
Downloads
Download


This work is licensed under a Creative Commons Attribution 4.0 International License.
Article
Parameter Learning of Probabilistic Boolean Control Networks with Input-Output Data
Hongwei Chen 1,*, Qi Chen 1, Bo Shen 1, and Yang Liu 2
1 College of Information Science and Technology, Donghua University, Shanghai 201620, China
2 School of Mathematical Sciences, Zhejiang Normal University, Jinhua 321004, China
* Correspondence: hongwei@dhu.edu.cn
Received: 23 September 2023
Accepted: 27 November 2023
Published: 26 March 2024
Abstract: This paper investigates the parameter learning problem for the probabilistic Boolean control networks (PBCNs) with input-output data. Firstly, an algebraic expression of the PBCNs is obtained by taking advantage of the semi-tensor product technique, and then, the parameter learning problem is transformed into an optimal problem to reveal the parameter matrices of a linear system in a computationally efficient way. Secondly, two recursive semi-tensor product based algorithms are designed to calculate the forward and backward probabilities. Thirdly, the expectation maximization algorithm is proposed as an elaborate technique to address the parameter learning problem. In addition, a useful index is introduced to describe the performance of the proposed parameter learning algorithm. Finally, two numerical examples are employed to demonstrate the reliability of the proposed parameter learning approach.
Keywords:
probabilistic boolean control networks parameter learning semi-tensor product forward and backward probabilities expectation maximization algorithm1. Introduction
The Boolean network (BN), as a typical logic model, was firstly put forward by Kauffman [1] with the aim of understanding the dynamics of nonlinear and complex biological systems. An important application of the BN is to simulate the dynamics of gene regulatory networks (GRNs) [2]. Understanding regulation mechanisms in GRNs plays a crucial role in practical applications. A new Boolean model, namely the Boolean control network (BCN), has been put forward in the pioneering work [3]. Recently, by taking advantage of the semi-tensor product (STP) of matrices, a novel method called the algebraic state space representation (ASSR) has been proposed to analyse the dynamics of BNs [4]. Consequently, the study of BNs has achieved great progress, such as controllability and observability [5, 6], disturbance decoupling [7, 8], synchronization [9, 10], optimal control [11, 12], output regulation [13, 14] and others [15−18].
A recent yet important discovery in the field of systems biology is that the gene expression process involves considerable uncertainties. Hence, a deterministic Boolean model might not be suitable for real applications. For the sake of simulating thee dynamics of actual GRNs accurately, the concept of probabilistic Boolean networks (PBNs) has been innovatively proposed by Shmulevich in [19]. The dynamics of PBCNs can naturally be regarded as a stochastic expansion of BCNs. Specifically, at each time step, the governing BCN is randomly selected from a collection of BCNs and endowed with a predetermined probability. In the past decades, much effort has been devoted to the study of PBNs and PBCNs, such as synchronization [20], finite-time stability [21], model evaluation [22], state feedback stabilization [23], optimal control [24], stability and stabilization [25, 26].
The parameter learning issue for BNs has emerged as a research topic of vital importance since it is helpful to reveal the regulatory principles of genes and uncover the regulatory process of GRNs. The key of the parameter learning problem lies in obtaining the parameters of BNs from time-series gene expression data. In other words, the identified BNs should match the given data as much as possible. In the past decades, a significant amount of attention has been focused on the parameter learning/identification issue of BNs from gene expression data. Based on the best-fit extension paradigm, some efficient algorithms have been proposed in [27] to identify the model structure, which are extremely useful in situations where the measurements of the gene expression are noisy. In the interesting paper [28], a simplified search strategy has been introduced for the identification of BNs, which greatly reduces the time required to learn the networks. Based on a novel representation method of PBNs, an efficient learning algorithm has been designed in [29] for predicting the dynamic behavior of big-scale logic systems. It is worth noting that the aforementioned identification algorithms of Boolean models only use information on the occurrence of samples. For the purpose of extending the identifiable classes, a novel approach has been established in [30] to identify a PBN from samples, which also makes use of the information on the frequencies of different samples.
By resorting to the STP technique, a logic function can be represented as an algebraic form, and a BN can naturally be transformed into a discrete-time linear system. Then, the parameter identification problem of BNs can be converted into the problem of identifying the parameter matrices of the linear system that has been established, which definitely makes the learning problem more accessible. Note that the parameter learning issue for BNs has emerged as a research topic of great importance. In recent years, many interesting results have been achieved regarding the parameter learning issue of BNs. In the pioneering work [31], an STP-based method has been developed to construct the dynamic model of BNs by using the observed data. Later, some necessary and sufficient conditions have been established to identify a BCN via a series of input-output data [32]. In order to lower the data requirements, a position-transform mining technique has been proposed in the work [33] to improve data utilization during the identification procedure. In the interesting paper [34], an integer linear programming approach has been utilized to identify BNs based on the time-series gene expression data and the prior knowledge of the partial network structure and interactions between nodes.
It is worth mentioning that PBCNs contain several inputs and uncertainties, which makes it difficult to learn the network. To the best of the authors’ knowledge, the parameter learning problem of PBCNs is still open and remains challenging. Therefore, the main motivation of this article is to shorten this gap by designing some effective parameter learning algorithms. The main technical contributions can be highlighted as follows: (1) the algebraic representation of PBCNs with input-output data is provided to simplify the learning problem; (2) two recursive STP-based algorithms are designed to calculate the forward and backward probabilities; (3) the expectation maximization (EM) algorithm is developed to learn the model parameters; and (4) a useful index is introduced to evaluate the performance of the proposed parameter learning algorithm.
The rest of this paper is arranged as follows. We introduce several fundamental preliminaries with respect to the ASSR of PBCNs and formulate the problem in Section 2. In Section 3, we present the main results of the parameter learning of PBCNs with input-output data and introduce an index to evaluate the performance of the developed parameter learning algorithm. In Section 4, two numerical examples are provided to demonstrate the validity of the proposed learning strategy. Section 5 gives a concise conclusion of this paper.
2. Preliminaries and Problem Statements
For convenience, we first introduce some necessary notations. 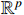 and
and  stand for the
stand for the  -dimensional Euclidean space and the set of all
-dimensional Euclidean space and the set of all  real matrices, respectively.
real matrices, respectively. 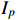 is the identity matrix with degree
is the identity matrix with degree 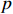 .
.  means the set of non-negative integers.
means the set of non-negative integers. 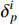 represents the
represents the  th column of
th column of 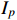 .
.  refers to the delta set
refers to the delta set 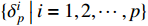 .
.  is called a logic matrix if
is called a logic matrix if  , where
, where 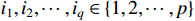 . For format compactness, the logic matrix
. For format compactness, the logic matrix  can alternatively be denoted as
can alternatively be denoted as  . The set of all logic matrices of dimension
. The set of all logic matrices of dimension  is denoted by
is denoted by 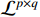 .
.
2.1. Mathematical Preliminaries
We present some indispensable preliminaries with respect to the STP technique, which will be quite instrumental in the subsequent study of the parameter learning problem.
Definition 1. [4] Let matrices  and
and 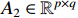 be given. Then the STP of
be given. Then the STP of 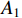 and
and 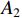 can be defined by the following formula:
can be defined by the following formula:

where  denotes the lowest common multiple of integers
denotes the lowest common multiple of integers 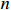 and
and 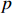 .
.
Remark 1. It is easy to see that the regular matrix multiplication can be regarded as a particular case of the STP of matrices. Therefore, the symbol “ ” can be omitted if no confusions arise.
” can be omitted if no confusions arise.
Lemma 1. [4] Some basic properties of the STP are listed as follows.
(i) Let 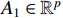 and
and 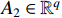 be two column vectors. Then,
be two column vectors. Then,
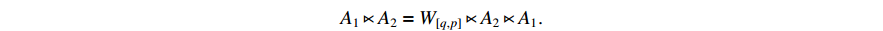
(ii) Let the 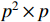 logic matrix
logic matrix 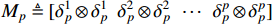 and
and  be given. Then,
be given. Then,

For convenience, the logic variable  is identified with the vector
is identified with the vector 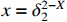 . Based on Lemma 1, a matrix expression of the logical functions is given as follows.
. Based on Lemma 1, a matrix expression of the logical functions is given as follows.
Lemma 2. [4] Let 
 be a logical function. Then, there exists a unique matrix
be a logical function. Then, there exists a unique matrix 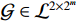 , namely, the structure matrix of
, namely, the structure matrix of 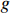 , such that
, such that
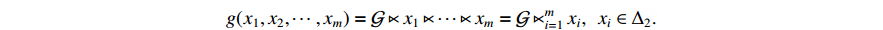
Consider a PBCN with 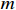 control inputs,
control inputs, 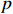 output nodes and
output nodes and  state nodes. The state equation with a control input can be written as
state nodes. The state equation with a control input can be written as
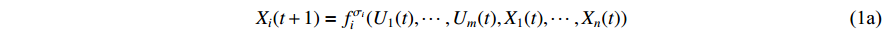
where  denotes the discrete time instant.
denotes the discrete time instant. 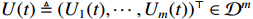 represents the control input which is assumed to be known and deterministic, and
represents the control input which is assumed to be known and deterministic, and  stands for the state vector. The logical functions
stands for the state vector. The logical functions 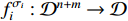 ,
, 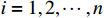 ,
,  , can be selected in the domain
, can be selected in the domain 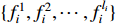 with certain probability
with certain probability 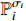 , and
, and 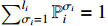 . In this paper, the choose of each constituent BN is assumed to be independent. It is easy to verify that there are
. In this paper, the choose of each constituent BN is assumed to be independent. It is easy to verify that there are  possible realizations for the network, and the probability of selecting the realization
possible realizations for the network, and the probability of selecting the realization 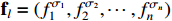 is
is 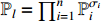 . The observation output equation can be written as
. The observation output equation can be written as
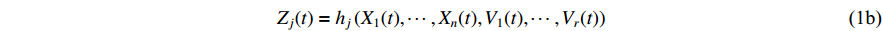
where the vector  refers to the measurement output at discrete time instant
refers to the measurement output at discrete time instant  .
. 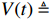 indicates the measurement noise obeying the Bernoulli distribution, i.e.,
indicates the measurement noise obeying the Bernoulli distribution, i.e., 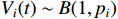 where
where  . The function
. The function 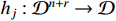 ,
, 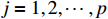 denotes the time invariant logical function.
denotes the time invariant logical function.
By taking advantage of the STP technique, the ASSR of system (1) can be obtained, which will essentially simplify the parameter learning problem investigated in this paper. Let  ,
, 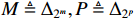 and
and 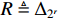 . By denoting
. By denoting 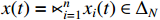 ,
, 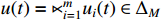 ,
, 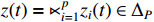 and
and 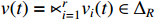 , one can obtain the componentwise algebraic form of system (1) as
, one can obtain the componentwise algebraic form of system (1) as

Based on Lemmas 1-2, the corresponding ASSR of system (1) can be obtained as follows:
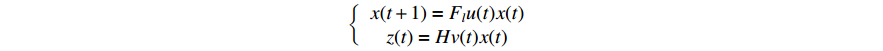
where 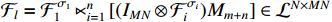 and
and 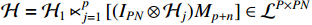 . Here,
. Here, 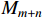 and
and 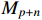 are the group power reducing matrices [4]. Let
are the group power reducing matrices [4]. Let 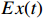 be the expectation value of the state variable
be the expectation value of the state variable 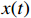 , we have
, we have

where 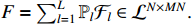
Based on the ASSR of the PBCNs, we can obtain the following auxiliary result whose proof is straightforward, and hence, omitted here for brevity.
Lemma 3. Consider the ASSR of system (2).
(i) For the given control input  , the one-step state transition probability that drives the state form
, the one-step state transition probability that drives the state form  to
to 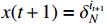 can be computed as follows:
can be computed as follows:
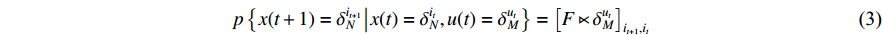
(ii) The observation probability can be calculated as follows:
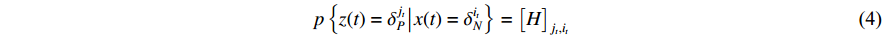
where 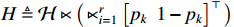 .
.
Remark 2. Lemma 3 implies that the state process is Markov and the observations are conditionally independent given the states.
2.2. Problem Formulation
For the PBCN (2), an important issue concerned in practical applications is to learn the model parameters which greatly match the observed output sequence. Actually, the dynamics of system (2) can be depicted by the state transition probability matrix 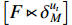 and the observation probability matrix
and the observation probability matrix 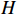 . Hereafter, the parameter learning problem of PBCNs is transformed into the problem of learning the above two probability matrices from the observed data. That is to say, instead of identifying system (1) directly, we are going to acquire its algebraic form (2) in the first step, and then, identify the corresponding system matrices. After that, it is possible to transfer the identified algebraic form (2) back into its logical form (1), see [35] for more details.
. Hereafter, the parameter learning problem of PBCNs is transformed into the problem of learning the above two probability matrices from the observed data. That is to say, instead of identifying system (1) directly, we are going to acquire its algebraic form (2) in the first step, and then, identify the corresponding system matrices. After that, it is possible to transfer the identified algebraic form (2) back into its logical form (1), see [35] for more details.
For convenience, the complete parameter set of the algebraic form (2) is denoted by 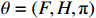 , where
, where 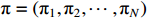 represents the initial distribution of the state and
represents the initial distribution of the state and  . The parameter
. The parameter  can be derived by maximum-likelihood estimation as follows:
can be derived by maximum-likelihood estimation as follows:
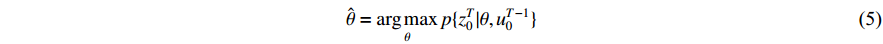
where 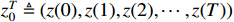 represents the observation sequence and
represents the observation sequence and  represents the control input sequence.
represents the control input sequence.
Problem 1. Given the observation sequence 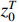 and control sequence
and control sequence 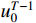 , the aim of parameter learning of PBCNs with input-output data is to learn the parameter
, the aim of parameter learning of PBCNs with input-output data is to learn the parameter  that maximizes the probability
that maximizes the probability  .
.
Remark 3. It is worth pointing out that the parameter learning problem for BNs can be addressed in two ways. The one is supervised learning, where many observation sequences and corresponding state sequences are known for inferring model parameters. The other is unsupervised learning, where only observation sequences are known for inferring model parameters.
3. Main Results
The above proposed parameter learning problem will be studied in this section. We will firstly establish some auxiliary results for computing forward and backward probabilities to facilitate the parameter learning of PBCNs. Subsequently, the EM algorithm will be implemented to learn the system matrix of system (2) in a computationally efficient way. Finally, an important index will be put forward to evaluate the performance of the proposed parameter learning algorithm.
3.1. Forward and Backward Probabilities in PBCNs
For the ease of notations, the state sequence  is denoted by
is denoted by 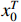 . Without loss of generality, we assume that
. Without loss of generality, we assume that 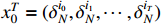 ,
, 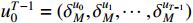 and
and  .
.
Theorem 1. Consider system (2) with the control sequence  and observation sequence
and observation sequence 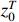 . The joint probability of the system state
. The joint probability of the system state 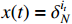 (
(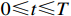 ) and the partial observation sequence
) and the partial observation sequence 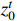 on the condition of
on the condition of  and
and 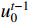 is denoted by
is denoted by

Then, the forward probability  can be computed in a recursive way as follows:
can be computed in a recursive way as follows:

with the initial condition 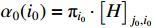 .
.
Proof of Theorem 1. According to the multiplication rule of probabilities and the definition of observation probabilities, the initial condition can be obtained as

Then, we prove the validity of the recurrence formula (7). It is apparent from (6) that
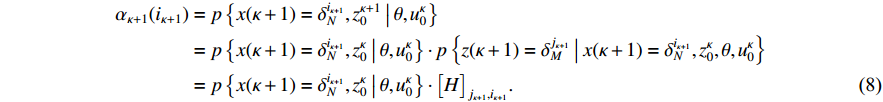
According to the total probability theorem and the definition of the one-step transition probability (3), we obtain
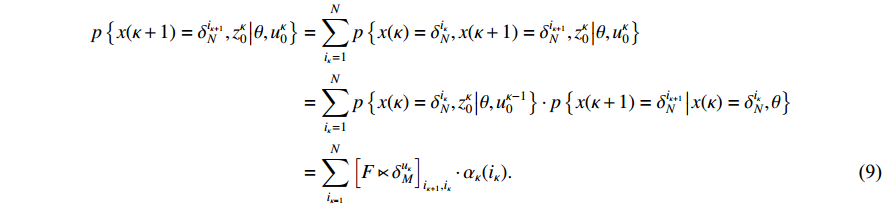
By substituting (9) into (8), the recursion (7) is verified, which completes the proof of Theorem 1.
Theorem 2. Consider system (2) with a control sequence 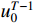 and an observation sequence
and an observation sequence  . The probability of observing
. The probability of observing 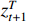 on the condition of
on the condition of 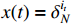 , the model
, the model 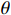 and the control sequence
and the control sequence  is denoted by
is denoted by
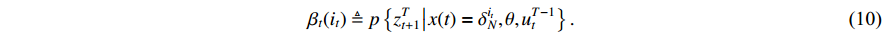
Then, the backward probability 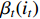 can be computed recursively as follows:
can be computed recursively as follows:
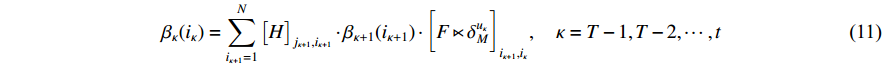
with the initial condition 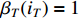 ,
, 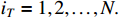
Proof of Theorem 2. It follows from (6) and (10) that
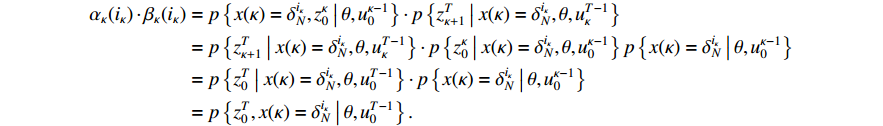
By letting  , we have
, we have

which implies that 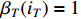 ,
, 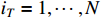 .
.
The next thing to do in the proof is to show the validity of the recursion (11). By resorting to the total probability theorem, we arrive at

It follows from the definition of the backward probability that
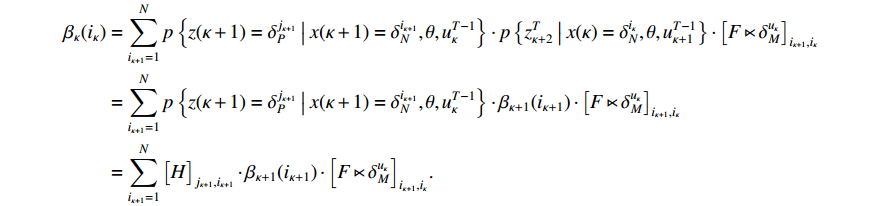
This completes the proof of Theorem 2.
Remark 4. The calculation process of the forward probability is based on the path of the state sequence. The key to the efficiency of the forward algorithm is to calculate the previous probability partially, and then use the path to recursively sum up the previous probability to avoid unnecessary repeated calculations. Specifically, we calculate  possible values of
possible values of 
 at the discrete time
at the discrete time  . Similarly, we calculate
. Similarly, we calculate 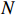 possible values of
possible values of  by adding up all the previous probabilities
by adding up all the previous probabilities 
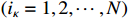 , which avoids the redundancy of repeated calculations. At the same time, the reason for high computational efficiency of the backward algorithm is also the same. Each step only depends on the result of subsequent steps without repeated calculations. As shown in Figure 1, when calculating the probability of one or more states, if we can make full use of forward and backward algorithms at the same time, the calculation complexity will be greatly reduced.
, which avoids the redundancy of repeated calculations. At the same time, the reason for high computational efficiency of the backward algorithm is also the same. Each step only depends on the result of subsequent steps without repeated calculations. As shown in Figure 1, when calculating the probability of one or more states, if we can make full use of forward and backward algorithms at the same time, the calculation complexity will be greatly reduced.

Figure 1. A trellis representation of the probability .
.
Theorem 3. By using the forward and backward probabilities, the specific formula for a single state probability can be obtained as follows.
(i) The probability of  on the condition of the observation sequence
on the condition of the observation sequence 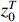 , the model parameter
, the model parameter  and the known control sequence
and the known control sequence  is denoted by
is denoted by 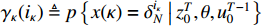 . Then, the probability
. Then, the probability  can be computed as follows:
can be computed as follows:
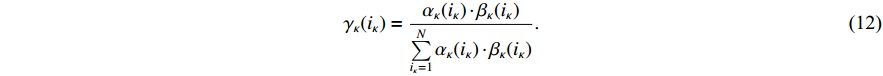
(ii) The joint probability of 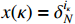 and
and  on the condition of the observation sequence
on the condition of the observation sequence 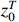 , the model parameter
, the model parameter 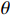 and the known control sequence
and the known control sequence  is denoted by
is denoted by 
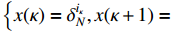 . Then, the probability
. Then, the probability  can be computed as follows:
can be computed as follows:

Proof of Theorem 3. According to the Bayesian formula, one has
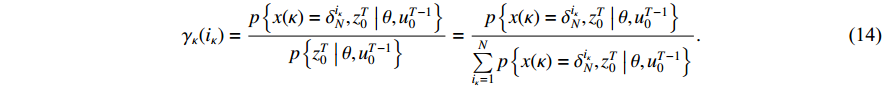
By the definition of  and
and 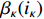 , it is not difficult to verify that
, it is not difficult to verify that
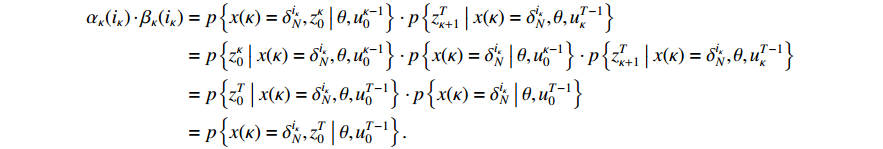
Taking (14) into consideration, we have (12).
We are now in the position to verify the correctness of (13). From the definition of  , we have
, we have
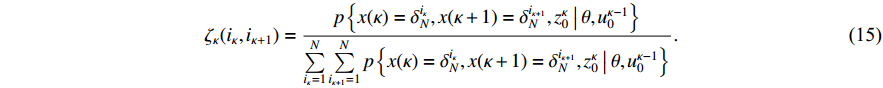
In the light of
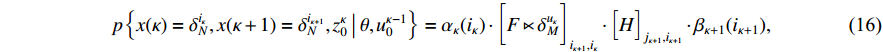
which, together with (15), implies that (13) holds. The proof is complete.
Remark 5. The forward and backward probabilities allow for the efficient computation of the likelihood of observed data, which is a critical component of the EM algorithm that will be discussed below. Instead of recomputing the probabilities from scratch at each iteration, the existing calculations are reused to make the algorithm significantly faster with the help of the forward and backward probabilities.
3.2. Parameter Learning of PBCNs
The EM algorithm, originally put forward by Dempster, is an iterative technique for computing maximum likelihood estimation with incomplete data [36]. The EM algorithm consists of two steps: an expectation step (i.e., the E-step) and a maximization step (i.e., the M-step) Algorithm 1. Specifically, the expectation is with respect to the latent variables, which utilizes the present estimate of the parameters conditioned on the observed data. The M-step provides a novel estimation of parameters. The two steps are iterated until convergence. We first define the incomplete data as  and complete data as
and complete data as  . Then, we can acquire the likelihood functions of the above two types of data, the likelihood function of the incomplete data
. Then, we can acquire the likelihood functions of the above two types of data, the likelihood function of the incomplete data 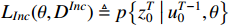 and the likelihood function of the complete data
and the likelihood function of the complete data  .
.
| Algorithm 1 EM algorithm for parameter learning of PBCNs |
Input: the observation sequence  and the control sequence and the control sequence  |
Output: the model parameters 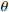 |
1: Randomly initialize 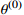 |
2: Set the maximum number of iterations 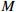 |
3: Set the convergence threshold  |
4: for  to to  do do |
5: if  then then |
6: for 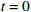 to to  do do |
| 7: E-step: |
8: compute 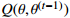 via (17) via (17) |
| 9: M-step: |
10: calculate 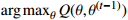 via (21) and (22) via (21) and (22) |
| 11: end for |
12: Set new  |
| 13: else |
14: Return optimal model parameters 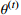 |
| 15: end if |
| 16: end for |
The EM algorithm for the parameter identification problem of PBCNs can be conducted as follows (provided in Algorithm 1). First, the algorithm will initialize the system parameter  . After that, the E-step and the M-step are alternated until the change of
. After that, the E-step and the M-step are alternated until the change of 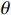 is less than a given threshold. Algorithm 1 shows the general progress of estimating the optimal parameter
is less than a given threshold. Algorithm 1 shows the general progress of estimating the optimal parameter 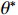 . Each step of the iteration will make the log-likelihood function increase and the algorithm will make the likelihood function approach to a local maximum value. In Algorithm 1, the
. Each step of the iteration will make the log-likelihood function increase and the algorithm will make the likelihood function approach to a local maximum value. In Algorithm 1, the 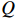 function is defined as follows:
function is defined as follows:
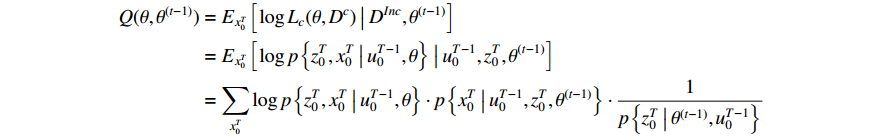
where 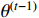 means the present parameter estimate and
means the present parameter estimate and 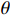 denotes the latest parameter that increases the value of
denotes the latest parameter that increases the value of 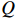 . It is obvious that
. It is obvious that  and
and 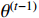 can be seen as constants, and
can be seen as constants, and  is the only variable required to be optimized. Note that the last term in the right-hand side (RHS) of the above equation can be treated as a constant. The
is the only variable required to be optimized. Note that the last term in the right-hand side (RHS) of the above equation can be treated as a constant. The 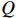 function can be simplified as
function can be simplified as
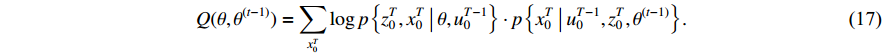
The next step is to find 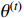 that maximizes the value of the
that maximizes the value of the 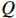 function (M-step), that is
function (M-step), that is

Given the state sequence and control sequence, we have
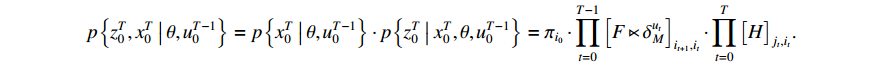
By taking the logarithm of the above expression, the 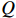 function can be rewritten as
function can be rewritten as
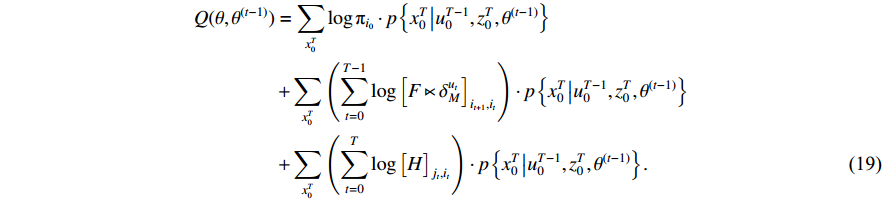
In view of the complexity of (19), we tend to, respectively, maximize the first term including 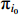 , the second term including
, the second term including 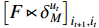 and the last term including
and the last term including  since they are independently unrelated.
since they are independently unrelated.
The first item of formula (19) can be rewritten as
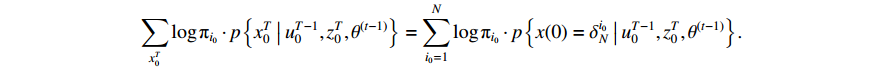
Since the initial probability distribution satisfies 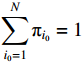 , we introduce the Lagrange multiplier
, we introduce the Lagrange multiplier  to generate the following Lagrange function. By taking the partial derivative of the Lagrange function with respect to the variable
to generate the following Lagrange function. By taking the partial derivative of the Lagrange function with respect to the variable  , we can obtain
, we can obtain
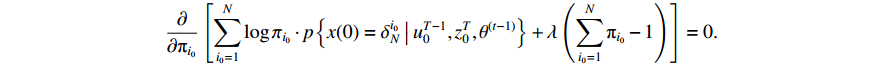
Then, let the value of the formula to be zero after conducting the partial derivative, and we have
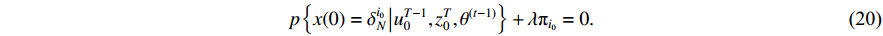
In the light of the fact that 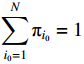 , we take the summation of equation (20) from
, we take the summation of equation (20) from  to
to  and obtain
and obtain 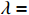 . Plugging the result into (20) yields
. Plugging the result into (20) yields

Moreover, combining the above result with equation (12), we have  .
.
Similarly, the middle item of formula (19) can be converted into the following form to determine 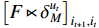 .
.
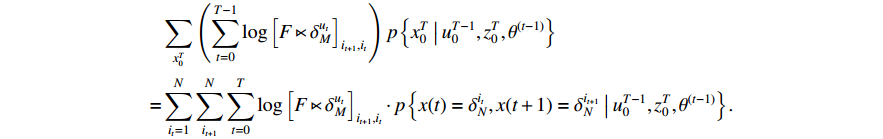
Then, it can be obtained by introducing another Lagrange multiplier and multiplying the restraint condition 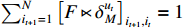 that
that
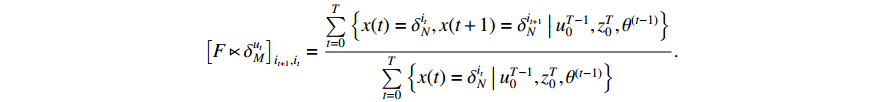
After applying the expressions of 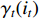 and
and 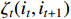 , we arrive at
, we arrive at

To find  , the third item of (19) can be transformed into
, the third item of (19) can be transformed into
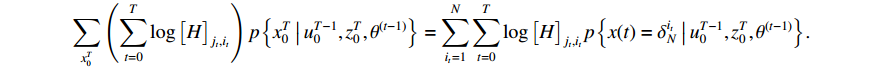
We can analogously introduce a Lagrange multiplier under the condition of 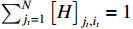 . Thus, there holds
. Thus, there holds
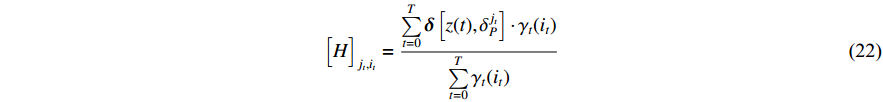
where 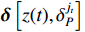 denotes the Kronecker delta function.
denotes the Kronecker delta function.
Remark 6. In the following, we introduce the index 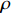 to describe the performance of the proposed parameter learning algorithm. Let the matrix
to describe the performance of the proposed parameter learning algorithm. Let the matrix  be the actual system parameter matrix and
be the actual system parameter matrix and 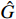 be the learned parameter matrix, and both matrices have
be the learned parameter matrix, and both matrices have 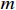 rows and
rows and 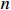 columns. Then, the index of the performance of the parameter learning algorithm can be defined as follows:
columns. Then, the index of the performance of the parameter learning algorithm can be defined as follows:
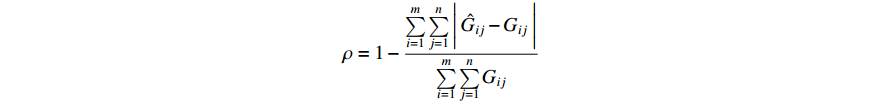
where  is the entry located in the
is the entry located in the  -th row and
-th row and  -th column of the matrix
-th column of the matrix 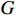 . It is not difficult to infer from the above definition that the parameter learning performance index
. It is not difficult to infer from the above definition that the parameter learning performance index 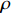 is theoretically a number more than
is theoretically a number more than 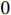 and less than
and less than 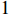 , without any unit. When the value of
, without any unit. When the value of 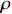 is more closer to 1, it means that the performance of the parameter learning algorithm is better, and vice versa.
is more closer to 1, it means that the performance of the parameter learning algorithm is better, and vice versa.
Remark 7. In fact, the transition probability matrix in the network that we learn can further be used to reconstruct the system back to the logic expression [35]. At the same time, the reconstruction process from the probabilistic state transition matrix to the PBCNs is not unique, so it is worth further improving the reconstruction algorithm of the logical expression of the PBCNs. More deeply, the reconstructed network cannot be completely consistent with the real network, so there is still much optimization work to be done in the process of network reconstruction.
4. Numerical Examples
Example 1. Consider a PBCN with 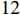 state nodes and
state nodes and 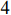 inputs. The network structure of the PBCN is shown in Figure 2, and the logic model is given as follows:
inputs. The network structure of the PBCN is shown in Figure 2, and the logic model is given as follows:
Figure 2. The model construction of the PBCN example in system (23).

The corresponding output observation equation can be described as

Based on Lemmas 1-2, the algebraic representation of model (23) can naturally be obtained as

where 
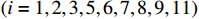 and
and 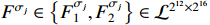
 .
.
Then, the following 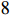 structure matrices can be calculated as
structure matrices can be calculated as
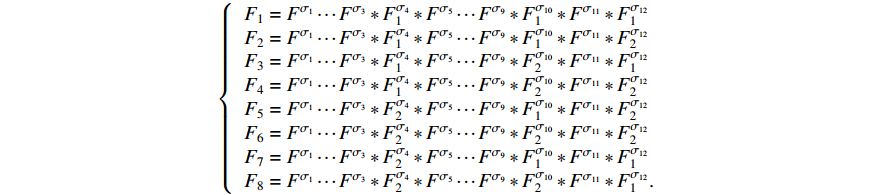
The algebraic representation form of model (23) can be written as
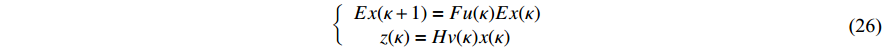
where the logic matrix 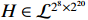 , the logic matrix
, the logic matrix  , and each probability satisfies
, and each probability satisfies

The measurement of the output observation value is shown in Figure 3 by resorting to the previously proposed algorithms to learn the parameter  under the designated output observation sequence. By resolving the former problem (5), we conduct three sets of parameter learning experiments and take the mean and variance at each iteration step. The mean value of the parameter learning performance index
under the designated output observation sequence. By resolving the former problem (5), we conduct three sets of parameter learning experiments and take the mean and variance at each iteration step. The mean value of the parameter learning performance index  of matrices
of matrices  and
and 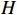 are
are 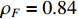 and
and 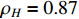 . As the iteration step increases, the parameter learning performance indexes of the two matrices continuously increase and finally stabilize at a certain high level shown in Figure 4.
. As the iteration step increases, the parameter learning performance indexes of the two matrices continuously increase and finally stabilize at a certain high level shown in Figure 4.
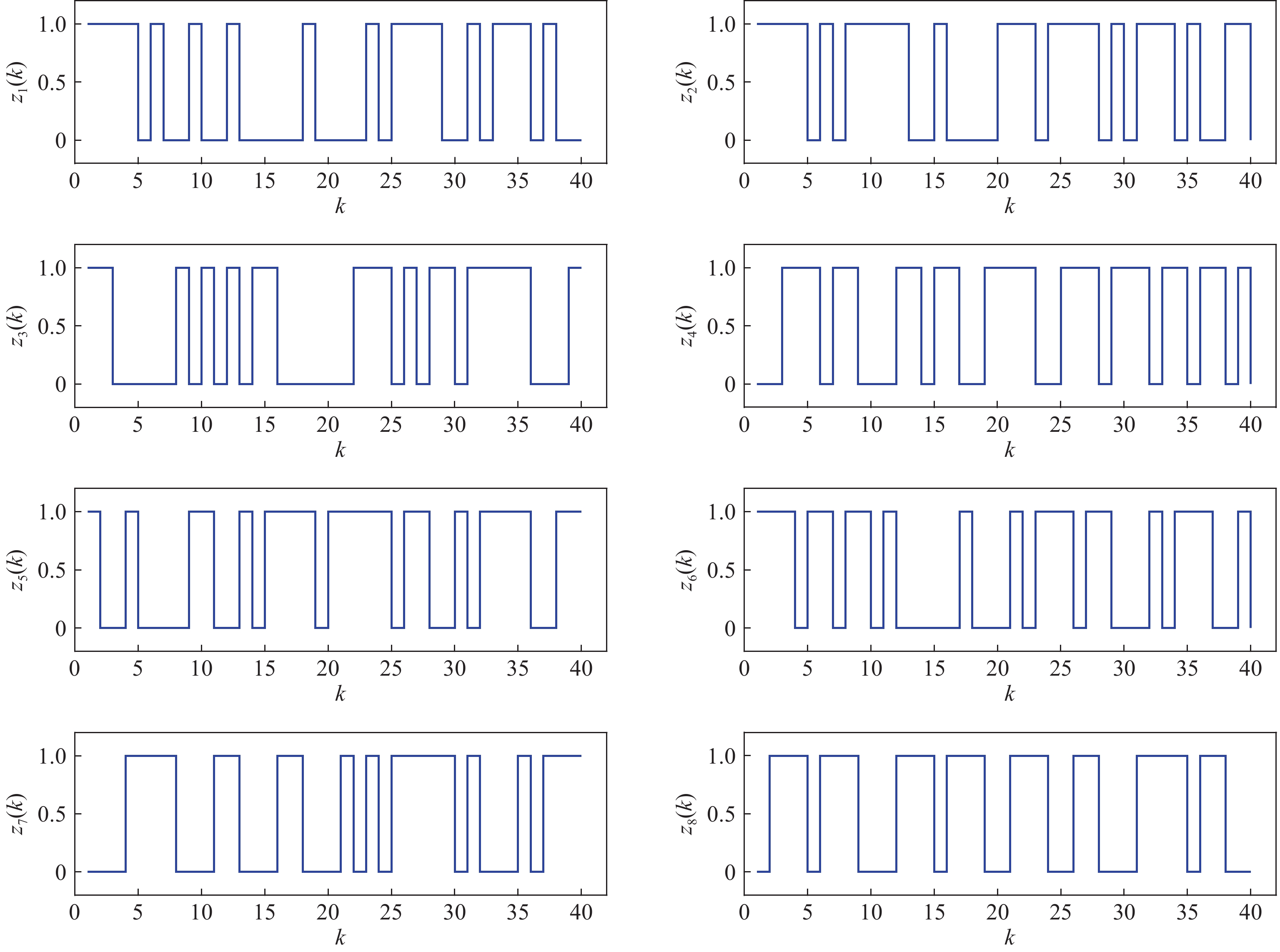
Figure 3. The measurement of the output observation value in system (24).
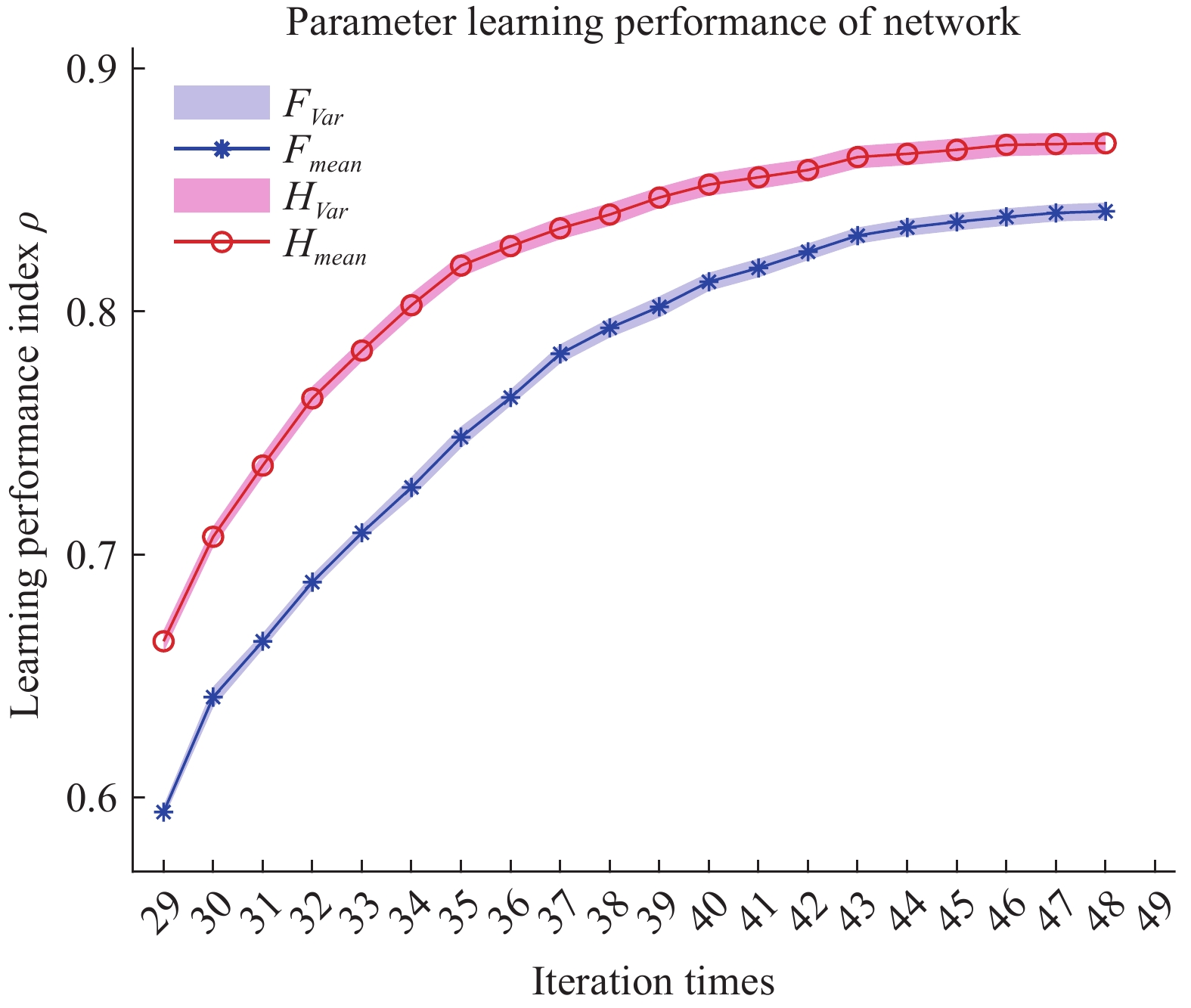
Figure 4. The parameter learning performance in system (26).
Example 2. We consider a PBCN originated from an actual  model, which is an essential biological regulatory network that keeps a fully functional organism. A faulty apoptotic network can lead to a variety of diseases with either insufficient apoptosis or excessive apoptosis [37]. Then, the logic model of the
model, which is an essential biological regulatory network that keeps a fully functional organism. A faulty apoptotic network can lead to a variety of diseases with either insufficient apoptosis or excessive apoptosis [37]. Then, the logic model of the  can be described as follows:
can be described as follows:
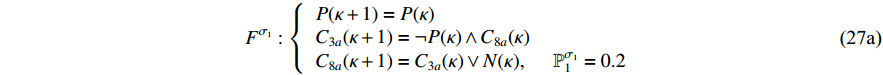
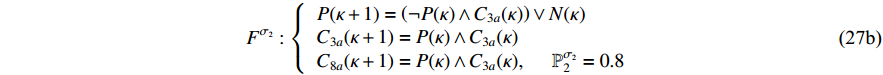
where  ,
,  and
and  indicate the active caspase 8 (C8a), active caspase 3 (C3a) and concentration degree in the inhibitor of apoptosis proteins, respectively; and
indicate the active caspase 8 (C8a), active caspase 3 (C3a) and concentration degree in the inhibitor of apoptosis proteins, respectively; and 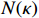 stands for the tumor necrosis factor's concentration degree. For the ease of notations, let
stands for the tumor necrosis factor's concentration degree. For the ease of notations, let 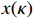 and
and  be, respectively, the state vector and control input vector of the apoptosis network, that is
be, respectively, the state vector and control input vector of the apoptosis network, that is  and
and 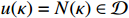 . System observations contain noise disturbances with
. System observations contain noise disturbances with 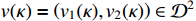 , where
, where  for
for 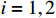 . The network structure of the PBCN (27) is shown in Figure 5. Each state node can freely switch its state in the range of network
. The network structure of the PBCN (27) is shown in Figure 5. Each state node can freely switch its state in the range of network  and
and 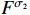 with the probabilities
with the probabilities 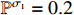 and
and  .
.
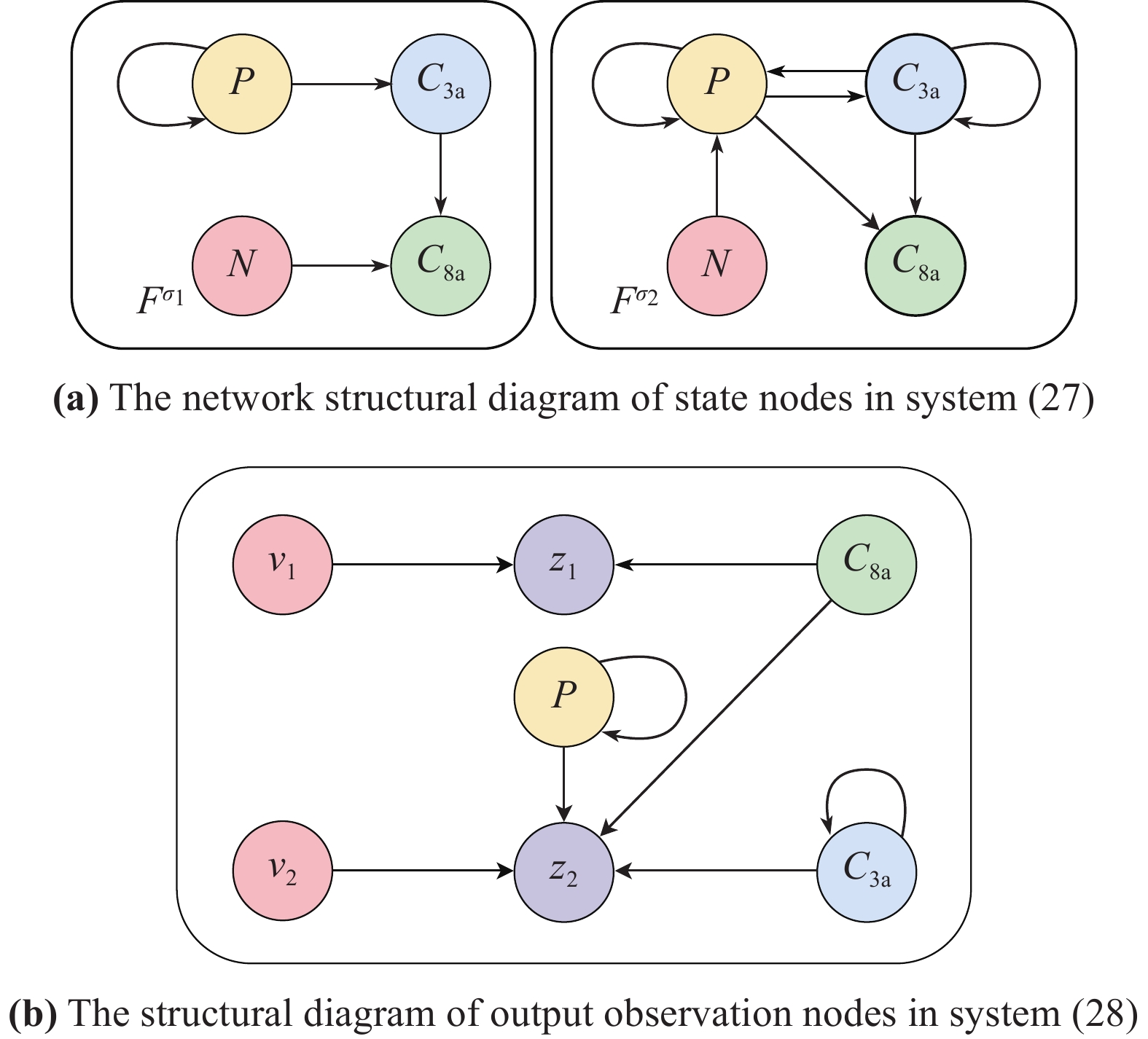
Figure 5. The network structure of PBCN in Example 4.
The output equation can be described as
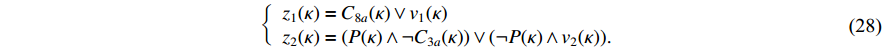
Let 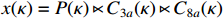 ,
,  ,
, 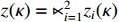 and
and 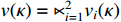 . With the help of the STP technique, the ASSR form of system (23) can be obtained as follows:
. With the help of the STP technique, the ASSR form of system (23) can be obtained as follows:

where
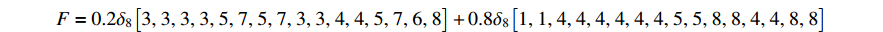
and
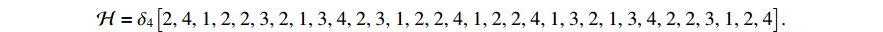
In the simulation, we take the control input sequence of the system as  and
and 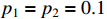 . Then, the observation probability matrix
. Then, the observation probability matrix  can be obtained as
can be obtained as

Figure 6 displays the observed output sequence 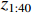 produced by the PBCN in (27) with the known observation probability matrix
produced by the PBCN in (27) with the known observation probability matrix 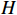 and state transition probability
and state transition probability 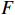 . The proposed algorithm is used to learn the matrices
. The proposed algorithm is used to learn the matrices 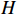 and
and 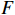 under the designated output observation sequence. Let
under the designated output observation sequence. Let  . The matrices can be estimated as follows:
. The matrices can be estimated as follows:
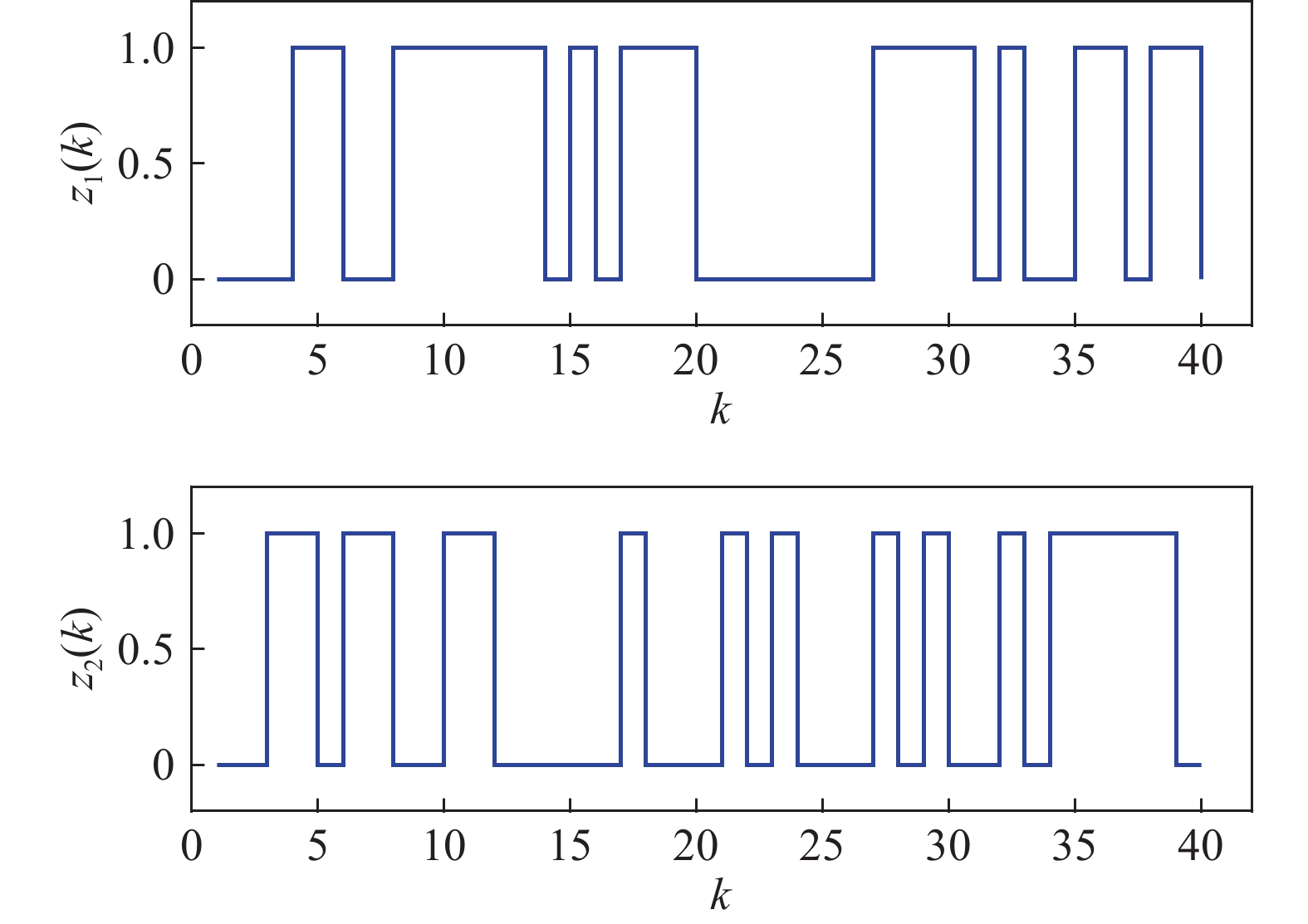
Figure 6. The measurement of the output observation value in system (28).


and
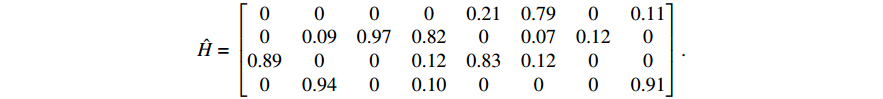
The parameter learning performance index  of matrices
of matrices  and
and 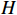 are
are 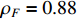 and
and 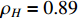 , respectively. The learning results of the above numerical example implies that our proposed algorithm performs well in identifying the model parameters under the real biological background.
, respectively. The learning results of the above numerical example implies that our proposed algorithm performs well in identifying the model parameters under the real biological background.
5. Conclusion
In this paper, the parameter learning problem has been investigated for PBCNs with input-output data. By utilizing the STP technique, the ASSR of PBCNS has been obtained. Based on it, the parameter learning problem has naturally been converted into the one of identifying the corresponding parameters of a linear system, which definitely makes the learning process more mathematically accessible. Subsequently, the STP-based recursive forward and backward algorithms have been proposed. Then, the EM algorithm has been utilized to deal with the parameter learning problem. After that, an index has been introduced to describe the performance of the designed parameter learning algorithms. Finally, a regular logical model and a GRN model of the biological cell apoptosis network have been employed to show the effectiveness of the developed parameter learning algorithms.
Author Contributions: Hongwei Chen: writing-supervision, review and editing of writing, funding acquisition; Qi Chen: original draft writing; Bo Shen: writing-supervision, review and editing of writing, funding acquisition; Yang Liu: writing-supervision, review and editing of writing, funding acquisition. All authors have read and agree to the final version of the manuscript.
Funding: The research was partially supported by the National Natural Science Foundation of China under Grant 62003083, in part by the Shanghai Science and Technology Program under Grant 20JC1414500, in part by the Fundamental Research Funds for the Central Universities, and in part by the DHU Distinguished Young Professor Program under Grant 23D210401.
Data Availability Statement: Not applicable.
Conflicts of Interest: The authors declare no conflict of interest.
References
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol., 1969, 22: 437−467. doi: 10.1016/0022-5193(69)90015-0
- Thomas, R. Boolean formalization of genetic control circuits. J. Theor. Biol., 1973, 42: 563−585. doi: 10.1016/0022-5193(73)90247-6
- Akutsu, T.; Hayashida, M.; Ching, W.K.; et al. Control of Boolean networks: Hardness results and algorithms for tree structured networks. J. Theor. Biol., 2007, 244: 670−679. doi: 10.1016/j.jtbi.2006.09.023
- Cheng, D.Z.; Qi, H.S.; Li, Z.Q.
Analysis and Control of Boolean Networks :A Semi-tensor Product Approach ; Springer: London, UK, 2011. doi: 10.1007/978-0-85729-097-7 - Cheng, D.Z.; Qi, H.S. Controllability and observability of Boolean control networks. Automatica, 2009, 45: 1659−1667. doi: 10.1016/j.automatica.2009.03.006
- Yu, Y.Y.; Meng, M.; Feng, J.E.; et al. Observability criteria for Boolean networks. IEEE Trans. Automat. Control, 2022, 67: 6248−6254. doi: 10.1109/TAC.2021.3131436
- Feng, J.E.; Li, Y.L.; Fu, S.H.; et al. New method for disturbance decoupling of Boolean networks. IEEE Trans. Automat. Control, 2022, 67: 4794−4800. doi: 10.1109/TAC.2022.3161609
- Zhao, R.; Feng, J.E.; Wang, B.; et al. Disturbance decoupling of Boolean networks via robust indistinguishability method. Appl. Math. Comput., 2023, 457: 128220. doi: 10.1016/j.amc.2023.128220
- Li, R.; Chu, T.G. Complete synchronization of Boolean networks. IEEE Trans. Neural Netw. Learn. Syst., 2012, 23: 840−846. doi: 10.1109/TNNLS.2012.2190094
- Chen, H.W.; Liang, J.L. Local synchronization of interconnected Boolean networks with stochastic disturbances. IEEE Trans. Neural Netw. Learn. Syst., 2020, 31: 452−463. doi: 10.1109/TNNLS.2019.2904978
- Fornasini, E.; Valcher, M.E. Optimal control of Boolean control networks. IEEE Trans. Automat. Control, 2014, 59: 1258−1270. doi: 10.1109/TAC.2013.2294821
- Laschov, D.; Margaliot, M. Minimum-time control of Boolean networks. SIAM J. Control Optim., 2013, 51: 2869−2892. doi: 10.1137/110844660
- Li, H.T.; Xie, L.H.; Wang, Y.Z. Output regulation of Boolean control networks. IEEE Trans. Automat. Control, 2017, 62: 2993−2998. doi: 10.1109/TAC.2016.2606600
- Zhang, X.; Wang, Y.H.; Cheng, D.Z. Output tracking of Boolean control networks. IEEE Trans. Automat. Control, 2020, 65: 2730−2735. doi: 10.1109/TAC.2019.2944903
- Zhang, Q.L.; Feng, J.E.; Wang, B.; et al. Event-triggered mechanism of designing set stabilization state feedback controller for switched Boolean networks. Appl. Math. Comput., 2020, 383: 125372. doi: 10.1016/j.amc.2020.125372
- Wang, Y.; Yang, Y.J.; Liu, Y.; et al. Fault detection and pinning control of Boolean networks. Appl. Math. Comput., 2022, 429: 127232. doi: 10.1016/j.amc.2022.127232
- Li, X.; Liu, Y.; Lou, J.G.; et al. Robust minimal strong reconstructibility problem of Boolean control networks. Appl. Math. Comput., 2023, 458: 128209. doi: 10.1016/J.AMC.2023.128209
- Li, H.T.; Xu, X.J.; Ding, X.Y. Finite-time stability analysis of stochastic switched Boolean networks with impulsive effect. Appl. Math. Comput., 2019, 347: 557−565. doi: 10.1016/j.amc.2018.11.018
- Shmulevich, I.; Dougherty, E.R.; Kim, S.; et al. Probabilistic Boolean networks: A rule-based uncertainty model for gene regulatory networks. Bioinformatics, 2002, 18: 261−274. doi: 10.1093/bioinformatics/18.2.261
- Chen, H.W.; Liang, J.L.; Lu, J.Q.; et al. Synchronization for the realization-dependent probabilistic Boolean networks. IEEE Trans. Neural Netw. Learn. Syst., 2018, 29: 819−831. doi: 10.1109/TNNLS.2017.2647989
- Li, H.T.; Yang, X.R.; Wang, S.L. Perturbation analysis for finite-time stability and stabilization of probabilistic Boolean networks. IEEE Trans. Cybern., 2021, 51: 4623−4633. doi: 10.1109/TCYB.2020.3003055
- Chen, H.W.; Wang, Z.D.; Shen, B.; et al. Model evaluation of the stochastic Boolean control networks. IEEE Trans. Automat. Control, 2022, 67: 4146−4153. doi: 10.1109/TAC.2021.3106896
- Li, R.; Yang, M.; Chu, T.G. State feedback stabilization for probabilistic Boolean networks. Automatica, 2014, 50: 1272−1278. doi: 10.1016/j.automatica.2014.02.034
- Wu, Y.H.; Guo, Y.Q.; Toyoda, M. Policy iteration approach to the infinite horizon average optimal control of probabilistic Boolean networks. IEEE Trans. Neural Netw. Learn. Syst., 2021, 32: 2910−2924. doi: 10.1109/TNNLS.2020.3008960
- Li, F.F.; Xie, L.H. Set stabilization of probabilistic Boolean networks using pinning control. IEEE Trans. Neural Netw. Learn. Syst., 2019, 30: 2555−2561. doi: 10.1109/TNNLS.2018.2881279
- Ding, X.Y.; Li, H.T.; Yang, Q.Q.; et al. Stochastic stability and stabilization of n-person random evolutionary Boolean games. Appl. Math. Comput., 2017, 306: 1−12. doi: 10.1016/j.amc.2017.02.020
- Lähdesmäki, H.; Shmulevich, I.; Yli-Harja, O. On learning gene regulatory networks under the Boolean network model. Mach. Learn., 2003, 52: 147−167. doi: 10.1023/A:1023905711304
- Nam, D.; Seo, S.; Kim, S. An efficient top-down search algorithm for learning Boolean networks of gene expression. Mach. Learn., 2006, 65: 229−245. doi: 10.1007/s10994-006-9014-z
- Apostolopoulou, I.; Marculescu, D. Tractable learning and inference for large-scale probabilistic Boolean networks. IEEE Trans. Neural Netw. Learn. Syst., 2019, 30: 2720−2734. doi: 10.1109/TNNLS.2018.2886207
- Akutsu, T.; Melkman, A.A. Identification of the structure of a probabilistic Boolean network from samples including frequencies of outcomes. IEEE Trans. Neural Netw. Learn. Syst., 2019, 30: 2383−2396. doi: 10.1109/TNNLS.2018.2884454
- Cheng, D.Z.; Qi, H.S.; Li, Z.Q. Model construction of Boolean network via observed data. IEEE Trans. Neural Netw., 2011, 22: 525−536. doi: 10.1109/TNN.2011.2106512
- Cheng, D.Z.; Zhao, Y. Identification of Boolean control networks. Automatica, 2011, 47: 702−710. doi: 10.1016/j.automatica.2011.01.083
- Zhang, X.H.; Han, H.X.; Zhang, W.D. Identification of Boolean networks using premined network topology information. IEEE Trans. Neural Netw. Learn. Syst., 2017, 28: 464−469. doi: 10.1109/TNNLS.2016.2514841
- Leifeld, T.; Zhang, Z.H.; Zhang, P. Identification of Boolean network models from time series data incorporating prior knowledge. Front. Physiol., 2018, 9: 695. doi: 10.3389/fphys.2018.00695
- Cui, L.B.; Li, W.; Ching, W.K. On Construction of sparse probabilistic Boolean networks from a prescribed transition probability matrix. In
Proceedings of the Fourth International Conference on Computational Systems Biology ,Suzhou ,China ,9–11 September 2010 ; ORSC & APORC, 2010; pp. 227–234. - Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. Roy. Stat. Soc.: Ser. B (Methodol.), 1977, 39: 1−22. doi: 10.1111/j.2517-6161.1977.tb01600.x
- Chaves, M. Methods for qualitative analysis of genetic networks. In
Proceedings of the European Control Conference ,Budapest ,Hungary ,23–26 August 2009 ; IEEE: New York, 2009; pp. 671–676. doi: 10.23919/ECC.2009.7074480





