Adaptive Output Feedback Tracking Control for Nonlinear Systems with Unknown Growth Rate

3.1. Observer Design

Article

Adaptive Output Feedback Tracking Control for Nonlinear Systems with Unknown Growth Rate

Manman Yuan ^1,2,*, and Wei Qian ^1,2,*

¹ School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, China

² Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment, Jiaozuo 454003, China

^* Correspondence: ymmamhappy@163.com; qwei@hpu.edu.cn

Received: 4 September 2023

Accepted: 7 November 2023

Published: 26 March 2024

Abstract: In this paper, the problem of adaptive output feedback tracking is considered for a class of nonlinear systems with lower-triangular structures. A novel dynamic gain is introduced to deal with the unknown growth rate. By coupling the dynamic gain with the observer and the controller, an adaptive output tracking controller is developed, which can guarantee that all signals of the closed-loop system are globally bounded. Finally, the effectiveness of the presented control scheme is illustrated by a numerical example.

1. Introduction

This paper considers the following nonlinear systems:

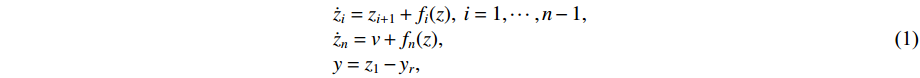
where ,  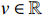and  are the system state, control input and measured output, respectively.  denotes the time-varying reference signal. , , 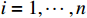are uncertain continuous nonlinear functions.

Owing to the incomplete measurability of all states in practical systems, the output feedback control method is an important and classical control approach in the control community [1–4]. Over the last decades, great efforts have been made on output feedback control for nonlinear systems [5–7]. Generally speaking, due to the non-separation principle, the output feedback control of nonlinear systems is difficult and challenging. By means of a sampled-data reduced-order observer, the problem of global stabilization was addressed in [6] for nonlinear systems. Under a linear growth condition, the problem of global exponential stabilization in the mean square sense was investigated in [7] for stochastic nonlinear systems by means of memoryless output feedback. In [8], a dual-domination method was presented to design an output feedback controller for nonlinear systems with unknown measurement sensitivity. By utilizing the method of output feedback domination, the considered nonlinear systems in [9] can achieve globally asymptotical stability. A novel sampled-data control scheme was put forward in [10] via the output feedback approach for nonlinear uncertain systems with and without designing any state observer. Note that in the above literature, the nonlinear terms of the studied systems satisfy the linear growth condition. Therefore, a problem naturally arises that when the restriction imposed on the nonlinear terms is relaxed, how to design an output feedback controller such that all states of the studied system are bounded?

As one of the fundamental control issues, the tracking control problem has drawn extensive attention due to its wide applications in dual-arm robots, autonomous surface vessels, motor-drive servo systems, and fixed wing unmanned aerial vehicles. Many excellent results have been reported on dealing with tracking problems of nonlinear systems [11–15]. In [12], by using a modified high-gain observer, a tracking control scheme was designed for a class of nonlinear systems subject to unknown parameters. By combining a neural network observer with the adaptive dynamic programming technique, the optimal tracking control algorithm was developed in [13] for continuous-time nonlinear systems. A novel formulation of the time-varying tracking control problem of high-order nonlinear systems was put forward in [14] with time-varying asymmetric output constraints. The authors of [16] investigated the problem of global practical output tracking for nonlinear systems with lower-triangular forms. In [17], the problem of global practical tracking control was addressed by virtue of the dynamic high-gain scaling method.

Inspired by the aforementioned analysis, the objective of this paper is to design a tracking control scheme for nonlinear systems with unknown growth rates. The main contributions of this paper can be summarized as the following three aspects. 1) The output tracking control problem of nonlinear systems is studied by utilizing the power integrator technique. 2) Compared with [8–10, 16], the nonlinear systems under consideration are more general as the included nonlinearities satisfy the homogeneous growth condition and have unknown growth rates. 3) A novel dynamic gain is designed to handle the unknown growth rate.

2. Preliminaries

We use the following assumptions and lemmas in analysis.

Assumption 1. For each 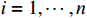, there exists an unknown constant  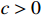such that

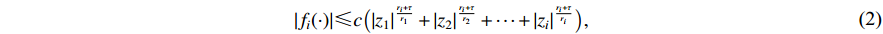
where 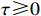 and  is defined by

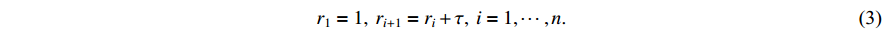
Assumption 2. The reference signal 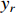 and its first-order derivative  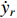are bounded.

Remark 1. It is worth noting that many systems may meet Assumption 1 in practice, such as the robotic systems and chemical systems. Compared with [8–10, 16], the growth condition given in Assumption 1 is weaker. Specially, when 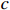 is a known constant and 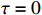, the growth condition reduces to the linear growth condition in [8, 9]; and when  is a known constant, the growth condition is equivalent to the condition given by Assumption 3.1 of [16].

Remark 2. Different from [15], Assumption 2 only requires the boundedness of  and 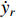, and is independent of the high-order derivatives of .

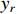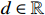Lemma 1. [18] For  and , if 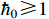, one has that

(i) ,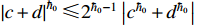

(ii) .

If 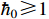 and 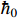 is a ratio of odd integers, one has that

(iii) ,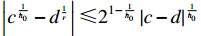

(iv) .

Lemma 2. [19] Assume 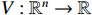 is homogeneous of the degree (HOD)  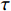with respect to the dilation 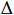. Then, we have that

(i) 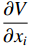 is HOD ;

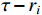(ii) for a constant , one has 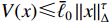. Assume that  is positive definite, then for 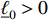, one has .

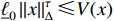Lemma 3. [18] For any 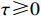, there exist constants , , such that the following system:

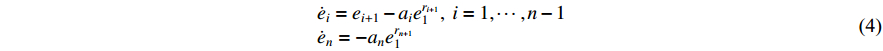
is globally asymptotically stable where 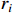 is the homogenous weight of  defined as

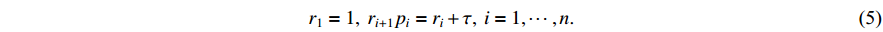
3. Main Results

For system (1), we design the following observer:

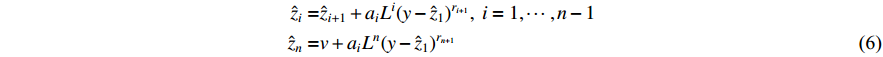
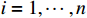where , constants , , are chosen according to [18], and  is a dynamic gain determined later. Then, a set of scaling-gain changes is introduced as follows:

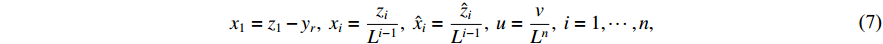
under which, system (1) becomes

where ,  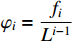and . Under the coordinate change (6) and Assumptions 1-2, there exist positive constants 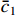 and 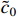 such that

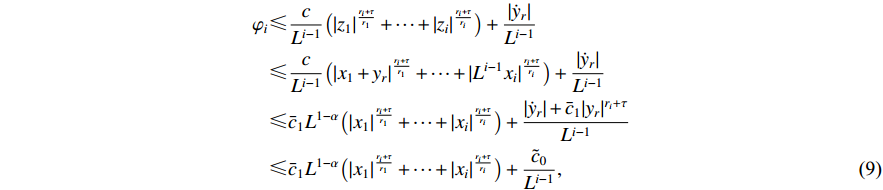
where .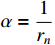

The above equation together with (6) and (7) leads to

Defining the observer error by , one has that

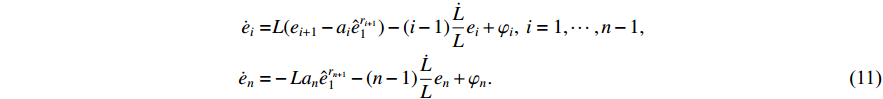
The following proposition is introduced, which can be obtained from [18] and [20].

Proposition 1. There exists a Lyapunov function 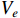 with an HOD  such that

where .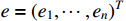

According to Lemma 2, there is a constant 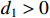 such that

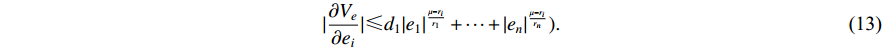
By weighted homogeneity, one has

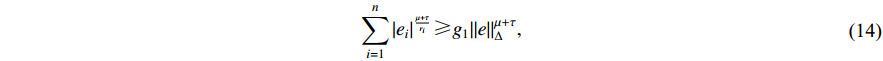
where  is a positive constant.

Define the following adaptive law:

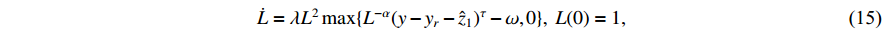
where 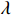 and  are two positive constants.

It can be deduced from Lemma 1 and (13) that

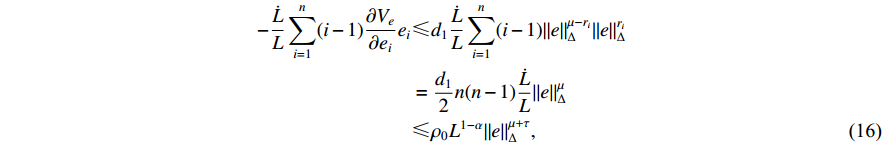
where 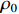 is a positive constant.

By Lemma 1 and Young's inequality, one has that

where  and  are constants.

By virtue of Young’s inequality, there exists a positive constant 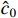 such that

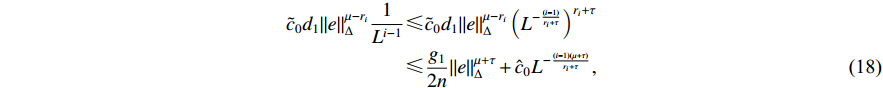
which together with (16) and (17) indicates

By (14), it can be seen that 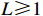. Then, (19) becomes

where .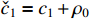

3.2. Controller Design

Choose the following Lyapunov function:

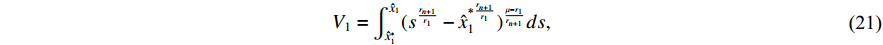
where 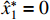. Its derivative is

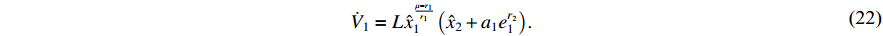
It follows from Young's inequality that

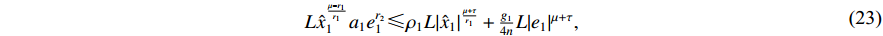
where .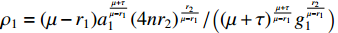

The virtual controller 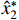 is defined as

where 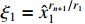. Then, it is not difficult to deduce that

Construct the following Lyapunov function:

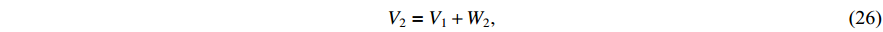
where . Then, the time derivative of  is calculated by

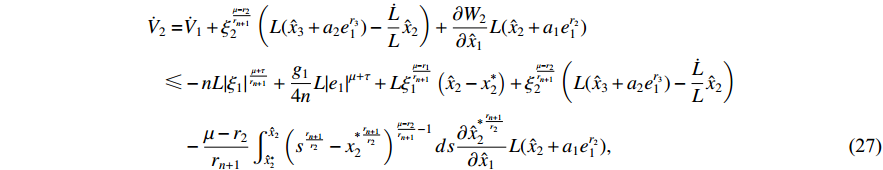
where .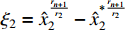

By using Young's inequality, it can be deduced that

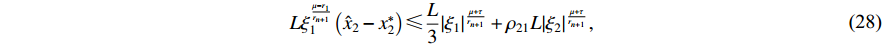
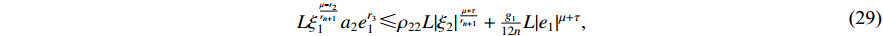
where 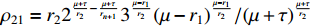 and .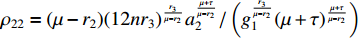

Similarly, we have that

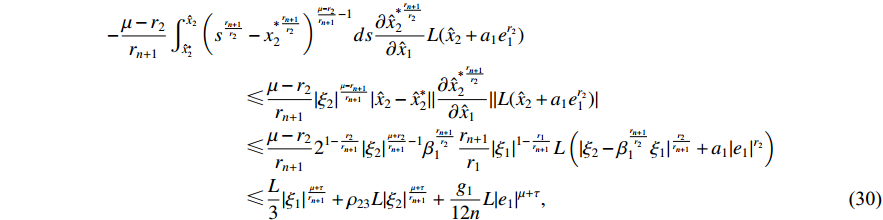
where 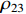 and  are two positive constants. Then, one can choose the virtual controller  as

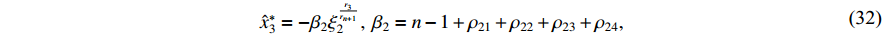
which guarantees

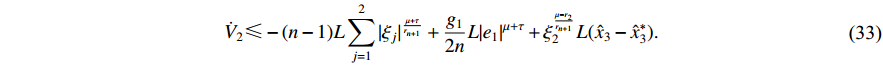
Suppose that at step 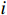, there is a Lyapunov function  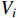and a set of virtual controllers  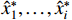defined by

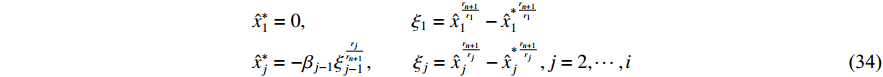
such that

where 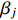 are positive constants.

Finally, at step 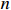, there exists a Lyapunov function

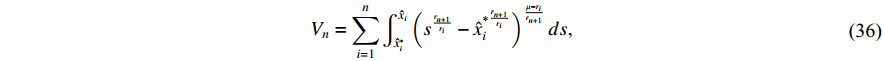
such that

Then, the controller is constructed as

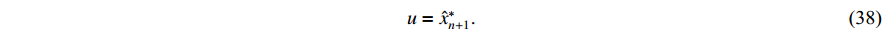
By weighted homogeneity, it can be inferred that

where 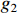 is a positive constant. Then, substituting (38) and (39) into (37) yields

Theorem 1. For system (1) satisfying Assumptions 1-2, the problem of global practical tracking can be solved by the adaptive output feedback controller comprised of (6), (15) and (38), and all signals of the closed-loop system are bounded.

Proof. Taking into account  and combining (20) and (40), we have

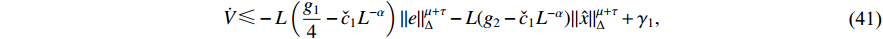
where 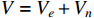 and .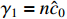

From the construction of , we have  and 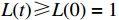. For any initial value , the resultant closed-loop system has a unique solution on the maximal existence interval 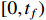. Then, we will prove that  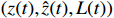is bounded.

Assume that 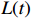 cannot escape at 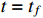. Due to 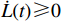,  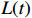is a monotonically nondecreasing function. Hence, there exists a time  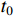such that

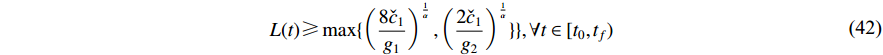
which together with (41) indicates

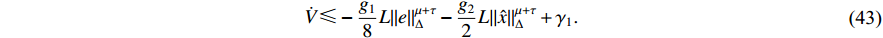
Thus, it is concluded that  is bounded on 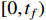. Suppose 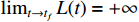. Recalling (15), one has 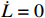, which contradicts the hypothesis that . Hence,  is bounded on . Based on (7), it is concluded that 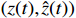 is bounded on 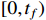. From the continuity of the solution, it can be deduced that . This implies that 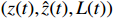 is bounded on .

Remark 3. As can be seen from Assumption 1, the growth rate 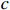 is unknown and its information cannot be directly utilized in controller design. This makes the controller design more difficult. As a consequence, a dynamic gain  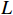is introduced to cope with the unknown growth rate.

Remark 4. In the controller design process, we have adopted the technique of adding a power integrator, which utilizes the homogeneous negative term 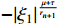 in (25) to dominate the superfluous term in the subsequent step.

4. Simulation Example

To illustrate the effectiveness of the proposed control approach, a numerical example is provided in this section.

Example 1. Consider the following system:

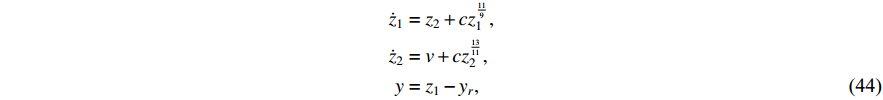
where 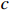 is an unknown constant. It is easy to see that Assumption 1 holds with .

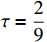The control aim is to track the reference signal 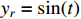. In the simulation, the parameters are set as 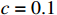, , 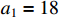, , , , 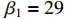 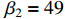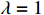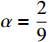and 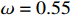. The initial conditions are , ,  and 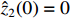. Simulation results are shown in Figures 1−3, from which it can be seen that all closed-loop signals are bounded. To illustrate the benefit of our controller, a comparative simulation is conducted between our control scheme and the control scheme in [16] with the same parameters. Figure 1 shows the response curves of the system state  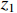and the reference signal 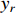. Clearly, our control scheme achieves better tracking performance than the scheme given by [16].

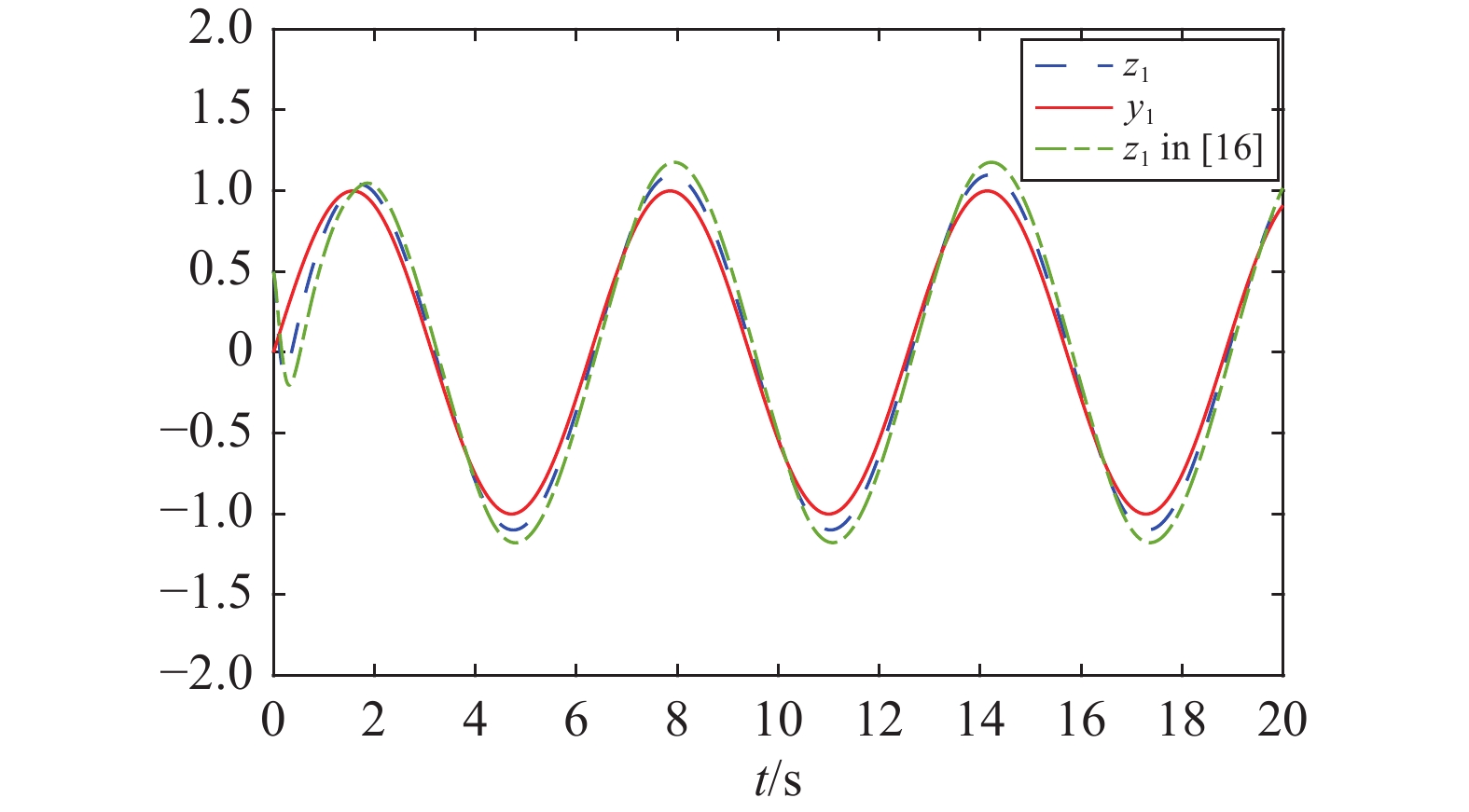
Figure 1. The curves of the system state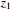and the reference signal .

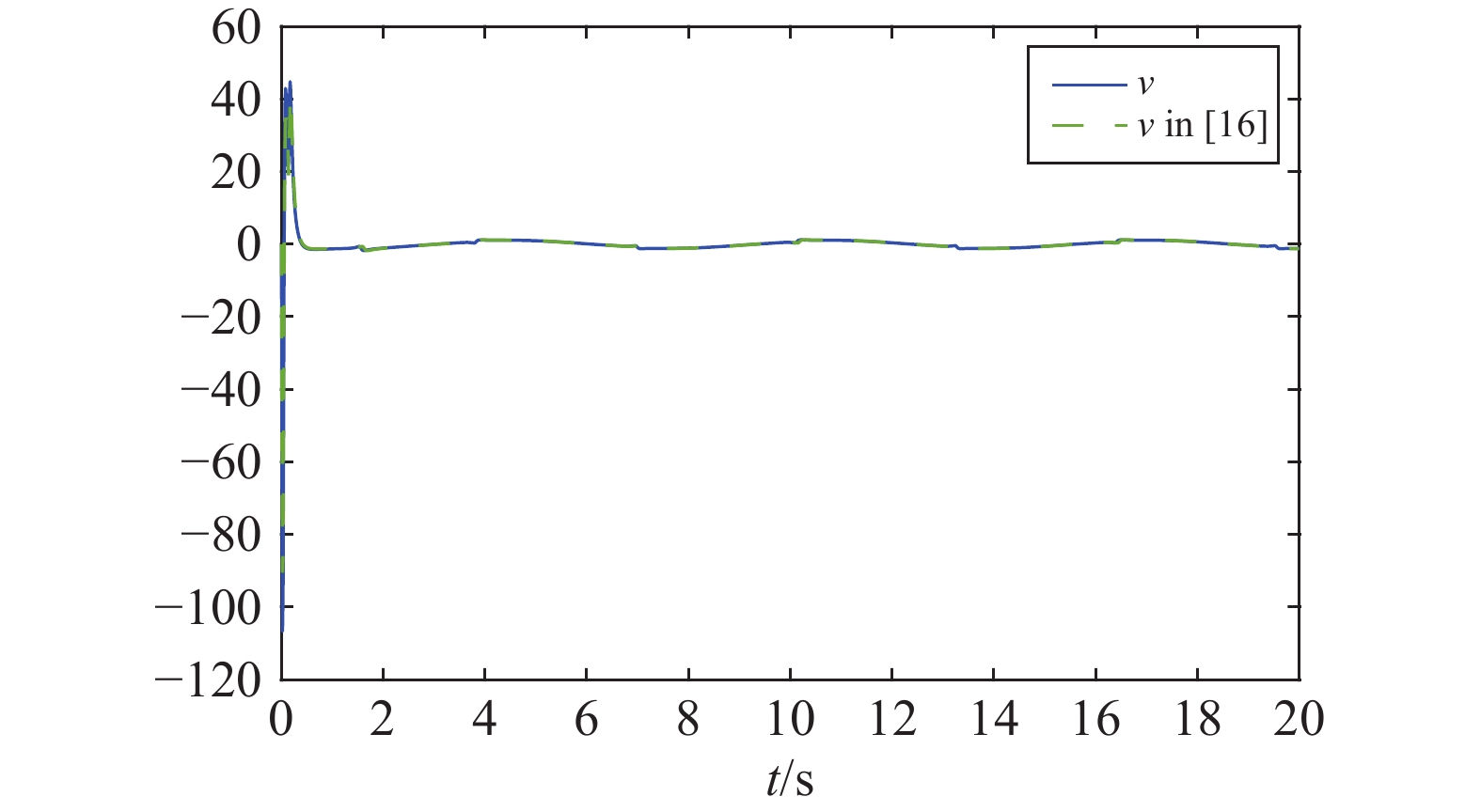
Figure 2. The curve of the control input .

Figure 3. The curve of the dynamic gain .

5. Conclusion

For a class of nonlinear systems with unknown growth rates, the tracking control problem has been solved via the output feedback strategy. A novel dynamic gain is introduced to eliminate the effect of the unknown growth rate. A dynamic-gain observer and an adaptive output feedback controller has been developed by means of adding a power integrator technique. A numerical example has been given to verify the validity of the presented result. Inspired by the current work, future work will focus on the prescribed-time fault-tolerant control of uncertain nonlinear systems.

Author Contributions: Manman Yuan: conceptualization, methodology, software, writing—original draft preparation, writing—reviewing and editing; Wei Qian: conceptualization, methodology, writing—original draft preparation. All authors have read and agreed to the published version of the manuscript.

Funding: This work was supported in part by the Plan of Key Scientific Research Projects of Colleges and Universities in Henan Province (24A120005).

Data Availability Statement: Not applicable.

Conflicts of Interest: The authors declare no conflict of interest.