
Downloads
Download


This work is licensed under a Creative Commons Attribution 4.0 International License.
Article
Predefined Time Fuzzy Adaptive Control of Switched Fractional-Order Nonlinear Systems with Input Saturation
Lusong Ding, and Weiwei Sun *
1 Institute of Automation, Qufu Normal University, Qufu 273165, China
* Correspondence: wwsun@hotmail.com
Received: 31 August 2023
Accepted: 31 October 2023
Published: 21 December 2023
Abstract: This article investigates the predefined-time fuzzy adaptive tracking control problem for a class of nonlinear switched fractional-order systems with input saturation and external disturbances under a nonstrict feedback structure. By combining the backstepping technique and the common Lyapunov function method, a predefined-time switching control method is constructed based on a novel fractional-order auxiliary function. The fuzzy logic system and the adaptive method are introduced to identify unknown compounded continuous functions. Moreover, the issue of calculating explosion and the problem of singularity are tackled through the newly proposed predefined-time and filter-based dynamic surface control. Especially, the construction of a continuous term in the controller eliminates possible chattering. The developed control strategy achieves that the closed-loop system is practically predefined-time stable under arbitrary switchings, where the upper bound of the settling-time can be defined by users in advance. Finally, two simulation examples are illustrated to prove the feasibility and effectiveness of the presented scheme.
Keywords:
adaptive control fractional-order systems predefined-time control input saturation switched system1. Introduction
Over the past decades, fractional-order systems have been widely studied in practical industrial areas, such as engineering, physics, biology, and chemistry. The fractional-order systems can depict and reflect the properties of objects more truly and accurately than the integer-order systems, thereby obtaining better control performance. Theoretical and practical research on fractional-order system control has attracted considerable interests, and different control approaches have been successfully applied including the sliding-mode control methods, robust control methods and adaptive control methods [1−3].
Owing to their strong learning and approximation abilities, fuzzy logic systems (FLSs) and neural networks (NNs) have been extensively used in the adaptive control of nonlinear systems to cope with dynamic uncertainties. The control performance of fractional-order systems has been improved by combining several advanced control methods. In [4] and [5], a robust adaptive control scheme was proposed for single-input single-output (SISO) fractional-order nonlinear systems by adopting the backstepping control technique. Such a scheme was extended in [6−8] to study multi-input multi-output (MIMO) fractional-order nonlinear systems. Considering the input nonlinearity and immeasurable states, the observer-based output feedback control scheme was presented in [6] for fractional-order nonlinear systems based on the fractional adaptive type-2 fuzzy technique. The adaptive decentralized control was investigated in [7] for nonlinear interconnected systems with mismatched interconnections. Furthermore, the fully distributed adaptive consensus tracking algorithm was proposed in [8] for nonlinear fractional-order multiagent systems subject to heterogeneous uncertainties.
In a variety of application scenarios, the input saturation is a commonly occurring nonlinearity and is considered to be a major threat to the control system [9−11]. The input saturation may be caused by the physical limitation of the actuator itself, or may be artificially introduced to prevent the excessive impact from destroying the stability of the actuator or even the system. Therefore, designing a suitable control approach for nonlinear systems with input saturation is an essential and necessary issue. By far, there have been two ways to handle the input saturation which include introducing an auxiliary system to the controller [12] or considering the presence of the saturation in the system [13]. Accordingly, the constraint control approach was designed in [14] for nonlinear fractional-order systems by considering the effect of the input saturation and state constraints whose extension to the nontriangular nonlinear systems was presented in [15]. Furthermore, an event-triggered control strategy was proposed in [16] which can dynamically adjust the threshold parameters according to the system output, thereby reducing the communication burden. Note that the above research work all focuses on nonswitched fractional-order systems.
It is generally known that the switched system, as a kind of hybrid system, is composed of exact switching rules and a series of switching subsystems, and has found widespread applications based on different controller switching strategies [17, 18]. Control schemes designed for switched systems are significant and challenging in various engineering control sytems, such as hybrid vehicle systems, robot control systems, and switching power converters [19, 20]. In [21], the common Lyapunov function approach was applied to solve the problem of global stabilization for arbitrary switching systems. The neuro-adaptive control method was proposed in [22] for switching nonlinear systems via the average dwell-time technique, and this method was successfully generalized to nonlinear switching fractional-order systems [23−25]. Nevertheless, the aforementioned work has focused relatively less on the time optimization problem of the control systems.
Generally, the actual system should be quickly stabilized to a stable operating region within a prescribed time in case of disturbances or uncertainties. Owing to its characteristics of fast response and disturbance rejection [26], the finite-time control strategy is suitable for keeping the control performance of nonlinear systems, and fruitful results have been obtained on the study of finite-time convergence [27, 28]. Note that the upper limited convergence time of the system is a bounded function depending on the initial values [29]. For many practical systems, the initial condition cannot be set arbitrarily to suit the actual needs, which limits the implementation of finite-time control. This motivates the study on fixed-time stability where the settling-time is independent of the initial value [30−32]. A noteworthy point is that both finite-time control and fixed-time control ignore the direct correlation between the bound of the convergence time and the designed system parameters, making it relatively challenging to search for parameters that satisfy the requirement of the convergence time.
To effectively reduce conservatism and easily adjust the convergence time bound, some researchers investigated the predefined-time Lyapunov stability [33−35] and developed practical predefined-time convergent adaptive control schemes for nonlinear systems [36−39]. Such a method further develops the predefined-time control theory. Among them, the adaptive predefined-time control scheme was designed in [36, 37] for nonlinear systems with the convergence time and tracking accuracy set artificially in advance. Furthermore, the new predefined-time filters were designed in [38, 39] to avoid problems of "explosion of complexity" and singularity. The predefined time control has the merit that the settling-time is determined only by the adjustment parameters relative to the finite/fixed time control, which means that the settling-time can be directly specified by adjusting the predefined time parameters. This attractive feature promotes the applications of predefined time control in a wide range of fields, such as tailless aircrafts [39], autonomous surface vehicles [40], and rigid spacecrafts [41]. Besides, a robust controller was designed in [42−44] with predefined-time convergence for fractional-order nonlinear systems, whereas the uncertainties and nonlinearities were not considered. So far, the predefined-time control has not attracted full attention for fractional-order nonlinear systems subject to input nonlinearities including input saturation, asymmetric time-varying constraints, and unknown control directions.
Motivated by the foregoing discussions, this study investigates a new predefined-time control scheme for uncertain MIMO switched fractional-order nonlinear systems with input saturation and external disturbances. Compared with the previous literature, the main contributions are given as follows.
1) In this paper, a novel fractional-order predefined-time control scheme is first developed based on an auxiliary function in a unified framework, where the convergence time explicitly appears as a tuning parameter. This scheme is applied to solve the tracking control problem for a class of switched fractional-order nonlinear systems, while the existing methods in [36−39, 42, 43] are not directly applicable to tackle the considered problem.
2) The presented fuzzy adaptive control scheme guarantees the control performance of closed-loop systems when arbitrary switching and input saturation happen, making it more generalized than the schemes in [6−8, 15, 16, 22].
3) An improved filtering technique is adopted to overcome the effect of repeated derivatives in the backstepping and singularity problems. Note that the chattering phenomenon may arise in the results of [36−39].
2. Problem Formulation and Preliminaries
2.1. Preliminaries
Definition 1. [45] For a real function  , the Riemann-Liouville (RL) fractional integral with fractional-order
, the Riemann-Liouville (RL) fractional integral with fractional-order 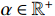 is defined as follows:
is defined as follows:

where 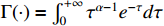 denotes the Gamma function.
denotes the Gamma function.
Definition 2. [45] The Caputo  -order fractional derivative for
-order fractional derivative for 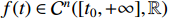 can be written as
can be written as
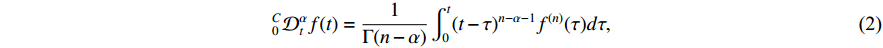
where  represents the
represents the  th order Caputo differential operator,
th order Caputo differential operator,  and
and  . This paper only considers the case of
. This paper only considers the case of 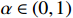 and
and  .
.
Property 1. [46] Assume that the Caputo fractional derivative  with
with  is integrable, then
is integrable, then

Particularly, if  , one has
, one has 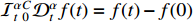 .
.
Lemma 1. [47] Suppose that  is a smooth and differentiable function vector, then
is a smooth and differentiable function vector, then  for
for 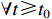 .
.
Lemma 2. [4] For  and a positive constant
and a positive constant  , one has
, one has

Lemma 3. [31] For any positive constants 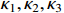 , the following inequality holds:
, the following inequality holds:

Lemma 4. [31] For 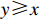 and
and 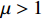 , the following inequality holds:
, the following inequality holds:

Lemma 5. [31] For a constant  with
with 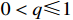 and
and 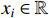 , the following inequality holds:
, the following inequality holds:

In the subsequently developed control design scheme, a fuzzy-approximation based approach is employed to approximate the continuous function. Note that FLSs have the following universal approximation property.
Lemma 6. [48] Suppose that 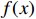 is a continuous arbitrary function defined in a compact set
is a continuous arbitrary function defined in a compact set  . For any small positive scalar
. For any small positive scalar 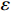 ,
,
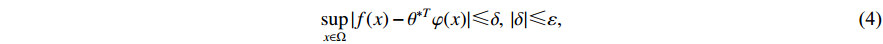
holds where 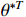 denotes the ideal constant weights,
denotes the ideal constant weights, 
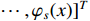 is the basis function vector with
is the basis function vector with  representing the number of the fuzzy rules, and
representing the number of the fuzzy rules, and 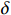 is the fuzzy minimum approximation error.
is the fuzzy minimum approximation error.
2.2. Predefined Time Stability Theory
Consider the integer-order system:

where  represents the system states,
represents the system states, 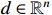 denotes the unknown but bounded disturbances, and
denotes the unknown but bounded disturbances, and 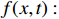 stands for the nonlinear function. We assume that the origin is the equilibrium point of system (
stands for the nonlinear function. We assume that the origin is the equilibrium point of system ( 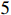 ).
).
Definition 3. [33, 34] For nonlinear system (5), the equilibrium point 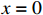 is fixed-time convergent if it is finite-time stable and there exists a bounded setting-time function
is fixed-time convergent if it is finite-time stable and there exists a bounded setting-time function 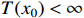 such that
such that  is bounded for
is bounded for 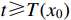 . If there exists a predefined time constant
. If there exists a predefined time constant 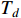 satisfying
satisfying 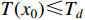 , then the origin of system (5) is predefined-time stable.
, then the origin of system (5) is predefined-time stable.
Lemma 7. [34] For dynamical system (5), if there exists a continuous and differentiable positive-definite function  such that
such that

where 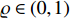 , and
, and 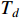 is the setting time. Then, the trajectory of system (5) is predefined-time stable.
is the setting time. Then, the trajectory of system (5) is predefined-time stable.
Theorem 1. For system (5), suppose that there exists a scalar function 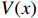 such that
such that

where 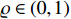 .
.  ,
, 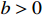 and
and  are the condition parameters for the convergence of the system. Then, the origin of system (5) is practically predefined-time stable. Besides, the solution
are the condition parameters for the convergence of the system. Then, the origin of system (5) is practically predefined-time stable. Besides, the solution 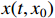 is bounded by
is bounded by

where 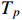 is the settling-time satisfying
is the settling-time satisfying 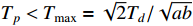 with
with 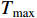 being the upper bound.
being the upper bound.
Proof 1. Now, consider the following two parts.
i) Inequality (7) implies
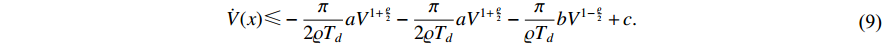
(9) can be rewritten as

for  . According to Lemma 7, it is obtained that system (5) is predefined-time stable with
. According to Lemma 7, it is obtained that system (5) is predefined-time stable with  , and the state trajectory
, and the state trajectory 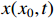 is bounded by
is bounded by  .
.
Integrating (10) over [0,  ], one has
], one has

which is followed by

where 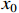 is the initial state during
is the initial state during  and
and 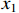 is the state when the system is stable during
is the state when the system is stable during  . Thus, the upper-bound settling time is given by
. Thus, the upper-bound settling time is given by  .
.
ii) It follows from (7) that
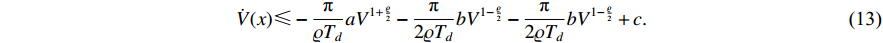
Similar to the previous proof, we know that the formula for calculating the convergence region is  with
with 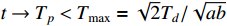 , which completes this proof.
, which completes this proof.
Remark 1. In Lemma 1, there exist two adjustable parameters 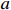 and
and  which makes the condition generally available for the actual system. Note that when
which makes the condition generally available for the actual system. Note that when 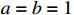 and
and  , the result in [34] is a particular case of Lemma 7. Thus, the existence of adjustable parameters
, the result in [34] is a particular case of Lemma 7. Thus, the existence of adjustable parameters 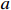 and
and 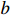 provides greater flexibility to the controller design than the fixed case of a=b=1. Further, the values of
provides greater flexibility to the controller design than the fixed case of a=b=1. Further, the values of 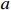 and
and  are the minimum gains of the controller. Compared with the results proposed in [39], the convergence time and convergence region of the system are much easier to be adjusted. Thus, the proposed scheme is suitable for wider application areas.
are the minimum gains of the controller. Compared with the results proposed in [39], the convergence time and convergence region of the system are much easier to be adjusted. Thus, the proposed scheme is suitable for wider application areas.
Remark 2. Note that Theorem 1 is a generalized form of Lemma 7 for the predefined time stability of integer-order systems. Due to the difference between integer-order calculus and fractional-order calculus, the results of predefined time stability of integer-order systems cannot be directly applied to fractional-order systems. Therefore, a novel fractional-order auxiliary function (20) is designed to solve this problem and guarantee the predefined-time stability of Caputo fractional-order systems.
Next, consider the following definition of the predefined-time convergence for fractional-order systems.
Definition 4. [42,43] Suppose that there is a fractional-order nonlinear system 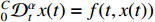 , where
, where  is the system state, and
is the system state, and 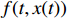 is a continuous function with
is a continuous function with  . Then, the solution will converge to
. Then, the solution will converge to  with the predefined-time
with the predefined-time  , if
, if  and
and  hold for
hold for 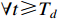 , where
, where  can be preassigned.
can be preassigned.
2.3. System Description
Consider a class of nonlinear nonstrict-feedback MIMO fractional-order switched systems composed of  subsystems. The
subsystems. The  th
th  subsystem is expressed by
subsystem is expressed by

where 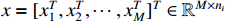

 is the system state variable, and
is the system state variable, and  is the system output variable.
is the system output variable.  stands for the switching signal with
stands for the switching signal with 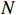 being the number of the subsystems, which is assumed to be a known piecewise continuous (from the right) function with respect to the time. When
being the number of the subsystems, which is assumed to be a known piecewise continuous (from the right) function with respect to the time. When 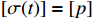 and
and  , it means that the
, it means that the 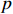 th subsystem is activated.
th subsystem is activated.  denotes an unknown smooth nonlinear function.
denotes an unknown smooth nonlinear function. 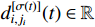 denotes the unknown but bounded external disturbance which is bounded by
denotes the unknown but bounded external disturbance which is bounded by 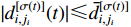 , where
, where 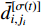 is an unknown constant
is an unknown constant 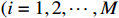 ,
,  .
.
Besides, 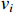 is the input signal of the controller.
is the input signal of the controller. 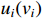 is the nonlinear saturation input of the
is the nonlinear saturation input of the 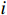 th subsystem, which is the output of the saturation nonlinearity described as follows [12]:
th subsystem, which is the output of the saturation nonlinearity described as follows [12]:
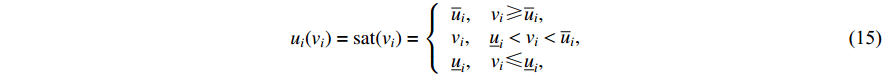
where  and
and  are bounds of
are bounds of  . To deal with non-tiny at sharp corners, a smooth hyperbolic tangent function
. To deal with non-tiny at sharp corners, a smooth hyperbolic tangent function 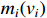 of the
of the  th system is denoted as follows:
th system is denoted as follows:

Accordingly, 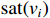 in (15) can be decomposed as
in (15) can be decomposed as

where 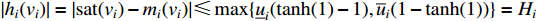 . By the mean-value theorem, we can get
. By the mean-value theorem, we can get 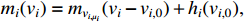
 and
and  with
with  .
.
By choosing 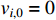 , we have
, we have

where  and
and 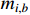 is an unknown positive constant.
is an unknown positive constant.
To design the adaptive tracking scheme for system (14), the following two common assumptions are required.
Assumption 1. For 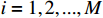 , the reference signal
, the reference signal  and its
and its  -order time-derivatives are continuous and bounded, i.e.,
-order time-derivatives are continuous and bounded, i.e.,  , where
, where  is a positive constant.
is a positive constant.
Control objective: we will design a practically predefined-time tracking control scheme for system (14) without violation of input saturation such that 1) the reference signal can be tracked by the system output in a predefined time and 2) all the closed-loop signals remain bounded.
3. Main Results
3.1. Controller Design
In this subsection, on account of the backstepping technology, the adaptive fuzzy predefined-time controller of system (14) is constructed for the 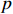 th activated subsystem.
th activated subsystem.
For  and
and  , define the following coordinates transformation:
, define the following coordinates transformation:
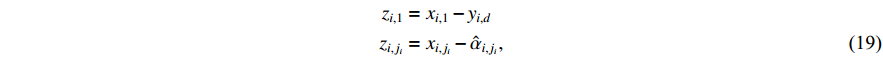
where 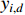 is a reference signal, and
is a reference signal, and 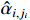 is the output of the first-order filter in connection with the virtual controller
is the output of the first-order filter in connection with the virtual controller  . The filtering error is defined by
. The filtering error is defined by  .
.
Besides, we introduce the following novel auxiliary function:
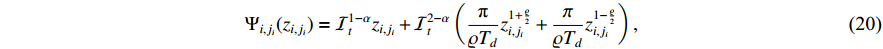
where  and
and 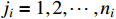 .
. 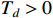 is a predefined parameter, and
is a predefined parameter, and 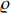 the ratio of two positive odd integers satisfying
the ratio of two positive odd integers satisfying 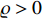 , which implies that
, which implies that 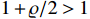 and
and  . Note that we assume the existence of a nonlinear function
. Note that we assume the existence of a nonlinear function  such that there exist strict positive constants
such that there exist strict positive constants 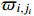 satisfying
satisfying 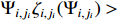 and
and 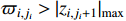 (
( 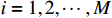 ,
, 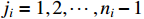 ). Then, we can deduce that the virtual control function
). Then, we can deduce that the virtual control function  for
for 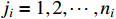 is
is
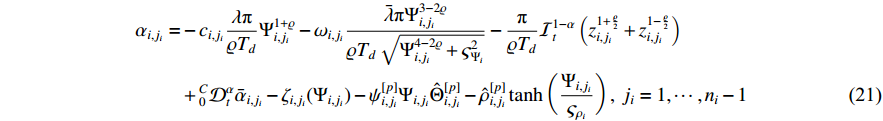
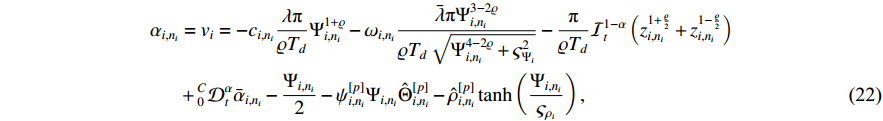
where 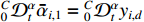 .
. 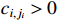 and
and  for
for 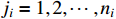 .
.  and
and 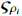 are the design constants.
are the design constants. 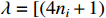 and
and  . Other parameters will be defined later.
. Other parameters will be defined later.
Step 1: When 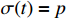 , according to (14) and (19), one can obtain the derivative of
, according to (14) and (19), one can obtain the derivative of 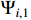 as
as
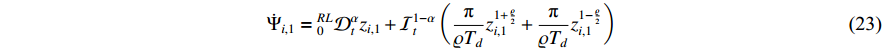
Putting  into
into 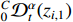 and substituting the error dynamics (19) into (23), one has
and substituting the error dynamics (19) into (23), one has

The candidate Lyapunov function is selected as

where 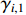 and
and 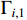 are positive design parameters.
are positive design parameters.  is the parameter estimation error.
is the parameter estimation error.  is the estimate of
is the estimate of  . Define
. Define 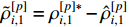 as the parameter error with
as the parameter error with  being the estimate of
being the estimate of  . Among them,
. Among them,  and
and  .
.
By Lemma 6, an FLS  is used to approximate
is used to approximate  . Based on (23) and Lemma 1, the time derivative of
. Based on (23) and Lemma 1, the time derivative of  can be calculated as
can be calculated as
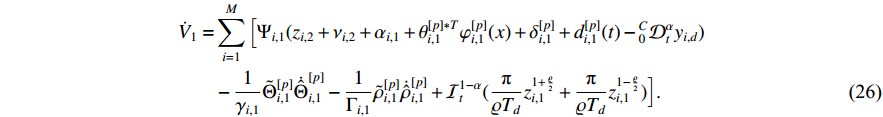
By means of Young’s inequality and the property of the fuzzy basis function  , one has that
, one has that
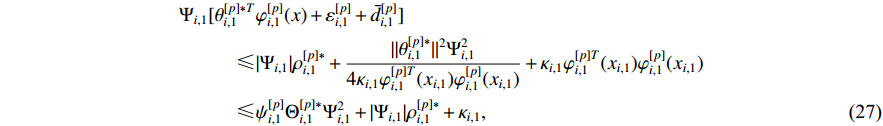
where  and
and  are positive constants to be designed.
are positive constants to be designed.
Substituting (27) into (26) yields

The parameter adaptive law is designed as


where 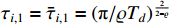 , and
, and  ,
, 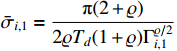 .
.
Recall the definition of 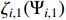 in (20), we have
in (20), we have

According to Lemma 2, substituting (21), (29)−(31) into (28) results in

where  .
.
Motivated by the work in [4], in order to reduce the computational complexity inherently embedded in the backstepping procedure, we propose a new predefined-time filter for fractional-order systems. Let  pass through the following predefined-time filter with a constant
pass through the following predefined-time filter with a constant  and a new state variable
and a new state variable 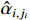 . The dynamics of
. The dynamics of 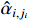 can be expressed as
can be expressed as
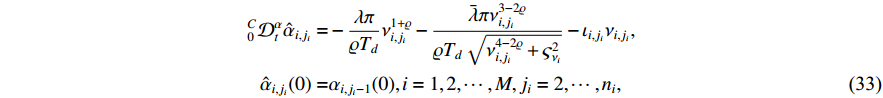
where  and
and  denote positive parameters to be designed. The
denote positive parameters to be designed. The 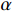 -th order derivative of the boundary layer errors
-th order derivative of the boundary layer errors  is
is
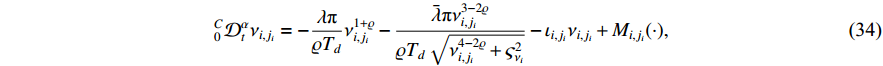
where  is a continuous function of the variables
is a continuous function of the variables 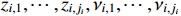 ,
, 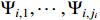 ,
, 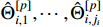 ,
,  and
and  . Meanwhile, there exists a positive constant
. Meanwhile, there exists a positive constant  such that
such that 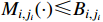 is a given compact set
is a given compact set  .
.
Step 
 According to the coordination transformation (19) and (20), one obtains
According to the coordination transformation (19) and (20), one obtains

by taking the time derivative of  .
.
To complete the induction, at the  -th step, we construct the following Lyapunov function:
-th step, we construct the following Lyapunov function:

where  and
and 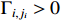 are parameters to be designed. Define
are parameters to be designed. Define  and
and  . Among them,
. Among them, 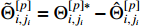 and
and 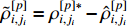 represent the parameter estimation errors with
represent the parameter estimation errors with  and
and 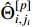 being the estimates of
being the estimates of 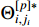 and
and  , respectively.
, respectively.
By (34) and (35), the derivative of 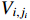 is
is
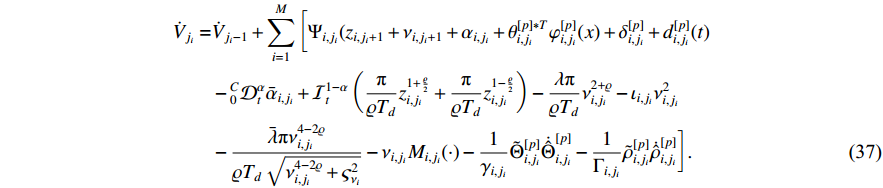
Using a similar procedure in Step 1, it can be verified that

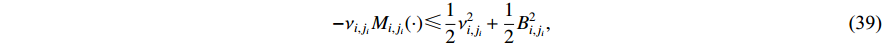
where 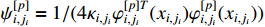 and
and 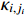 is a positive constant.
is a positive constant.
Putting together (37), (38) and (39) yields
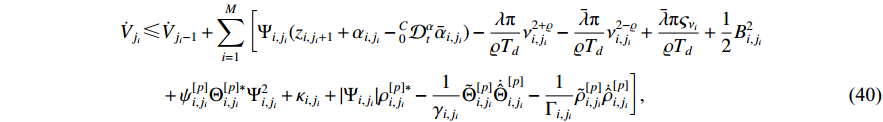
Design the parameter adaptation functions as

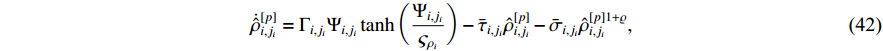
where 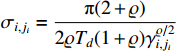 ,
, 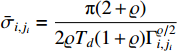 and
and  .
.
Similar to the previous step, by the definition of 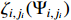 , we have
, we have

Substituting (21), (41)−(43) into (40) results in

where  .
.
Step  : In what follows, the derivative of
: In what follows, the derivative of  can be formulated by
can be formulated by
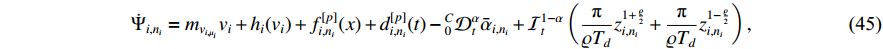
Consider the Lyapunov function candidate as follows:
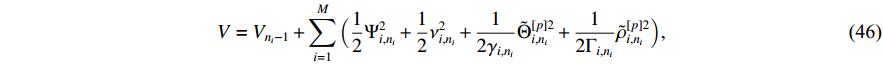
where  and
and 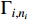 are positive constants.
are positive constants.
The following inequalities hold:
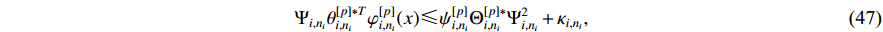



where 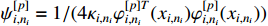 and
and  is a positive parameter.
is a positive parameter.
By differentiating the Lyapunov function 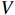 and using (47)−(50), it can be obtained that
and using (47)−(50), it can be obtained that

where  and
and 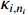 is a positive constant.
is a positive constant.
According to (51), the adaptive updated laws are designed as follows:
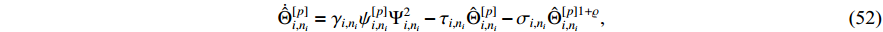
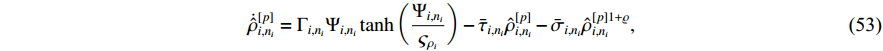
where 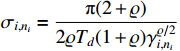 ,
, 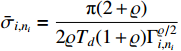 and
and 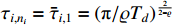 .
.
From the definition of  , substituting (22), (52)−(53) into (51), one has
, substituting (22), (52)−(53) into (51), one has

where 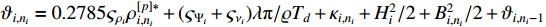 .
.
3.2. Stability Analysis
In this subsection, the stability of the considered system is readily verified. The major result of the proposed design is stated in the following theorem.
Theorem 2. Consider switched fractional-order system (14) with input saturation (15) under Assumption 1. Given predefined-time filter (33), actual controller (22), intermediate control functions (21), and parameter adaptation functions (29), (30), (41), (42) and (52) and (53), then all the closed-loop signals remain bounded and closed-loop system (14) is practically predefined-time stable. Furthermore, the tracking error can tend to a small region of the origin within a predefined time, and the impact of the input saturation is compensated simultaneously.
Proof 2. Applying Young’s inequality to (54) yields  , and
, and 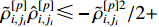 . Substituting the above two inequalities into (54), one has
. Substituting the above two inequalities into (54), one has
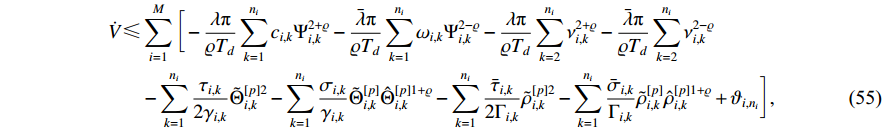
where  .
.
Furthermore, applying Lemma 3 to the above inequality, we have
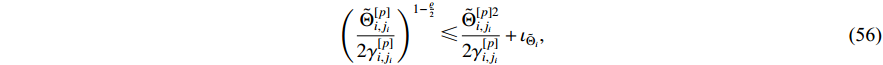
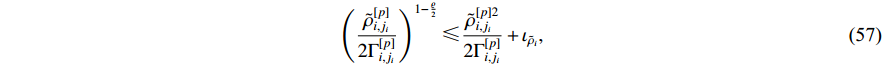
where  and
and 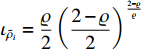 .
.
Consequently, with the help of Lemma 4, we have

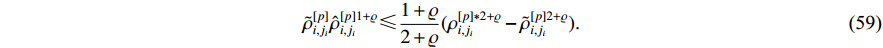
By further substituting (56)-(59) into (55), it can be deduced that

where 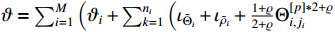
 .
.
Let 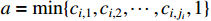 and
and  . Then, according to Lemma 5, one can easily obtain
. Then, according to Lemma 5, one can easily obtain

According to Theorem 1, it is known that for any 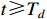 , the solution of system (14) will converge to the following compact set:
, the solution of system (14) will converge to the following compact set:

where the settling-time is given by  .
.
According to the definition of  , it is concluded from (61) that the auxiliary function
, it is concluded from (61) that the auxiliary function 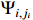 , adaptive parameter errors
, adaptive parameter errors 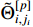 and
and 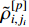 (
(  ,
,  ), and filtering errors
), and filtering errors  (
( 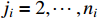 ) reach the boundary of
) reach the boundary of  after a predefined time. Taking into account
after a predefined time. Taking into account 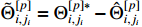 and
and 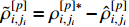 , the boundedness of
, the boundedness of  and
and  can be guaranteed. Then, the virtual control functions
can be guaranteed. Then, the virtual control functions 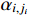 and
and 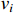 also remain bounded. Furthermore, from the definitions of the auxiliary function and the coordinate transformation, it can be concluded that all closed-loop signals of system (14) remain bounded. In other words, when the error variables are located at the auxiliary function, we have
also remain bounded. Furthermore, from the definitions of the auxiliary function and the coordinate transformation, it can be concluded that all closed-loop signals of system (14) remain bounded. In other words, when the error variables are located at the auxiliary function, we have  for
for 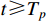 . When
. When 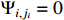 , the following equation holds:
, the following equation holds:
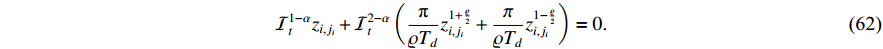
Taking the 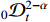 derivative and using the properties of the RL derivative, the following equation holds:
derivative and using the properties of the RL derivative, the following equation holds:
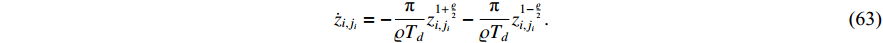
Based on Lemma 7, we can prove that 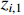 is predefined-time convergent. When the auxiliary function satisfies
is predefined-time convergent. When the auxiliary function satisfies  ,
, 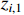 will converge to zero after a predefined-time which is bounded by
will converge to zero after a predefined-time which is bounded by 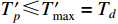 . From the initial time
. From the initial time  , the tracking error
, the tracking error 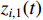 is achieved by the predefined-time, and the settling-time upper boundary is predetermined as
is achieved by the predefined-time, and the settling-time upper boundary is predetermined as  by designers. The proof is completed.
by designers. The proof is completed.
Remark 3. In fact, compared with the first-order linear filter commonly used in the dynamic surface control techniques for integer-order systems, the proposed predefined-time filter is designed for fractional-order systems and is able to directly set the convergence time of the filtering error. Such a filter also eliminates the complexity explosion problem caused by repeatedly deriving the intermediate control law during the backstepping recursive design procedure. Owing to the existence of the term , the derivative of the filtering error tends to infinity when tends to zero, and the singularity problem is avoided by using the function in this paper.
Remark 4. is the -order RL derivative. From Definition 1-2 and Property 1, it is known that in (23) coincides with the -th order RL derivative other than the -th order Caputo derivative, i.e. . According to the relationship between the Caputo and RL derivatives, if , we have . It is clear from the above description that, if , one can immediately have . Indeed, the term will monotonically decrease towards as time goes to infinity.
Remark 5. In Eqs. (20), (31) and (43), we suppose that the coefficient is greater than the maximum of the absolute error , which implies that the error , , is a priori bounded. This fact is usually possible since the solution of a fractional-order system is restricted to a bounded domain. Meanwhile, the effective determination of the parameter deserves attention in practice, and relative results can be found in many available applications. For example, the trial-and-error method can be successfully used to determine the actual value of the parameter [32].
Remark 6. So far, most of the results on predefined time control have designed their controllers based on the sign function [39−41, 43]. Although the fast convergence behavior is achieved, the chattering phenomenon still exists. Therefore, similar to [4], we introduce a function to avoid the possible chattering phenomenon. Note that cannot be too small; otherwise, the existence of the term will lead to the occurrence of the chattering phenomenon.
Remark 7. For switched nonlinear systems, the proposed method uses the common Lyapunov function approach (see [17,21, 23−25]) to construct the adaptive switching control law instead of using the multiple Lyapunov function approach and the average dwell time theory [18, 22]. As a result, the switching signal is no longer required to satisfy the predefined dwell time.
Remark 8. In fact, the radius of the tracking error region is determined by the control parameters. To guarantee a small tracking error, it is necessary to increase the values of parameters , and , or decrease the values of parameters , , , , and . Note that if the controller's predetermined time or the saturation value of the selected actuator is not reasonable, then the required stable time exceeds the actuator's capability.
4. Simulations
This section illustrates the applicability and effectiveness of the proposed control strategy by two simulation examples.
Example 1: Consider the following MIMO switched nonstrict feedback nonlinear system [23]:

where  denotes the switching signal.
denotes the switching signal.  ,
,  ,
,  and
and  .
. 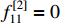 ,
, 
 and
and 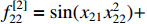 . We chose the external disturbances as
. We chose the external disturbances as 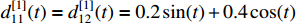 ,
,  ,
, 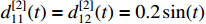 and
and  . The switching signal is selected as
. The switching signal is selected as 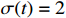 in
in  ;
; 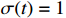 , otherwise.
, otherwise.
The design parameters of this example are chosen as 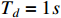 ,
, 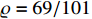 ,
, 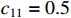 ,
,  ,
,  ,
,  ,
, 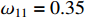 ,
,  ,
, 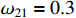 ,
, 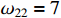 ,
, 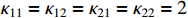 ,
,  and
and 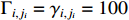 . The choice of parameters
. The choice of parameters 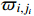 depends on the maximum values of the errors. In anticipation, we set
depends on the maximum values of the errors. In anticipation, we set 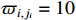 . The nonlinear functions
. The nonlinear functions  are chosen as
are chosen as  . The conditions
. The conditions  are well satisfied. In this example, the Gaussian membership functions are defined as
are well satisfied. In this example, the Gaussian membership functions are defined as  with
with  ,
, 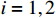 and
and  which are uniformly distributed on
which are uniformly distributed on 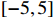 . The initial condition is chosen as
. The initial condition is chosen as  ,
, 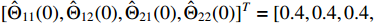 and
and 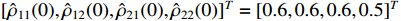 . The input saturation limits are set as
. The input saturation limits are set as 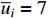 and
and 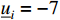 .
.
The simulation results are shown in Figures 1−6. Figure 1 depicts the tracking performance of the presented control strategy. It is observed that the trajectories of the reference signals  (
(  = 1, 2) can be tracked rapidly and precisely, illustrating the rationality of the designed filter. Figure 2 shows the trajectories of state variables
= 1, 2) can be tracked rapidly and precisely, illustrating the rationality of the designed filter. Figure 2 shows the trajectories of state variables  . The adaptive parameters
. The adaptive parameters 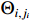 and
and  (
(  = 1, 2;
= 1, 2;  =1,2) are presented in Figure 3. Figure 4 displays the curves of controllers
=1,2) are presented in Figure 3. Figure 4 displays the curves of controllers 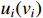 and
and 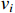 , which are constrained by input saturation with
, which are constrained by input saturation with 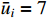 and
and  . As depicted in these figures, it is obvious that the practical settling time is less than the predefined time
. As depicted in these figures, it is obvious that the practical settling time is less than the predefined time 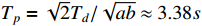 . The practical convergence time of the tracking error is much less than
. The practical convergence time of the tracking error is much less than 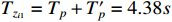 . Moreover, for the case that the switching signal occurs before the practical settling time, it follows from Figures 5 and 6 that, the tracking errors and filtering errors at different settling times
. Moreover, for the case that the switching signal occurs before the practical settling time, it follows from Figures 5 and 6 that, the tracking errors and filtering errors at different settling times 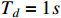 ,
, 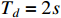 and
and 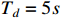 can all be retained to zeros within a small region, but variations exist in the convergence rate. According to Figure 6, we can see that the new filtering algorithm proposed in this paper can directly set the convergence time of the filtering error. Hence, it can be concluded that the proposed control method achieves the control objective successfully.
can all be retained to zeros within a small region, but variations exist in the convergence rate. According to Figure 6, we can see that the new filtering algorithm proposed in this paper can directly set the convergence time of the filtering error. Hence, it can be concluded that the proposed control method achieves the control objective successfully.
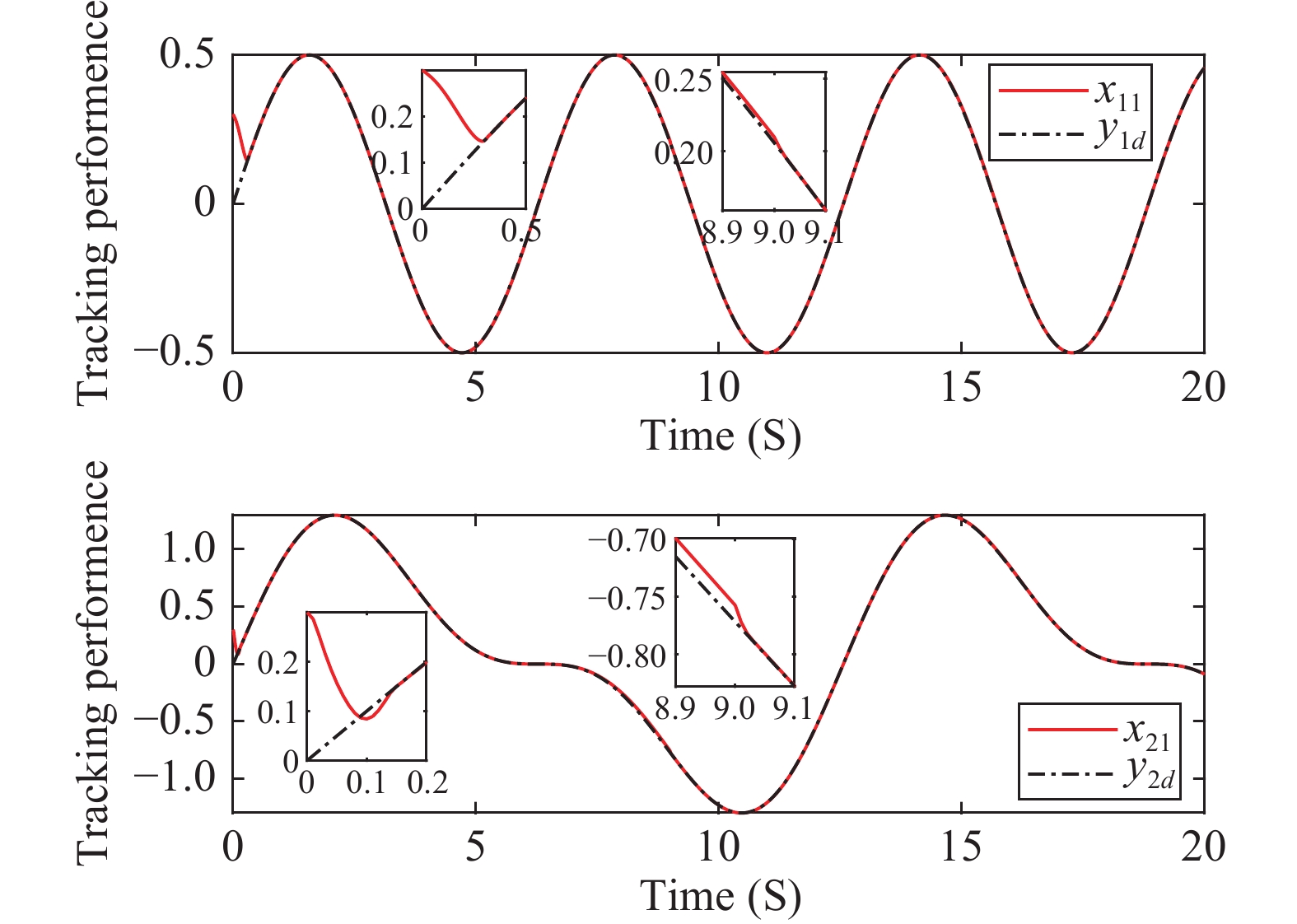
Figure 1. Example 1: Trajectories of system output and the reference signal
and the reference signal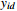 (
( =1, 2).
=1, 2).

Figure 2. Example 1: Trajectories of state variables and
and .
.

Figure 3. Example 1: Trajectories of the adaptive parameters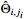 and
and (
(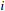 =1, 2;
=1, 2;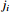 =1, 2).
=1, 2).
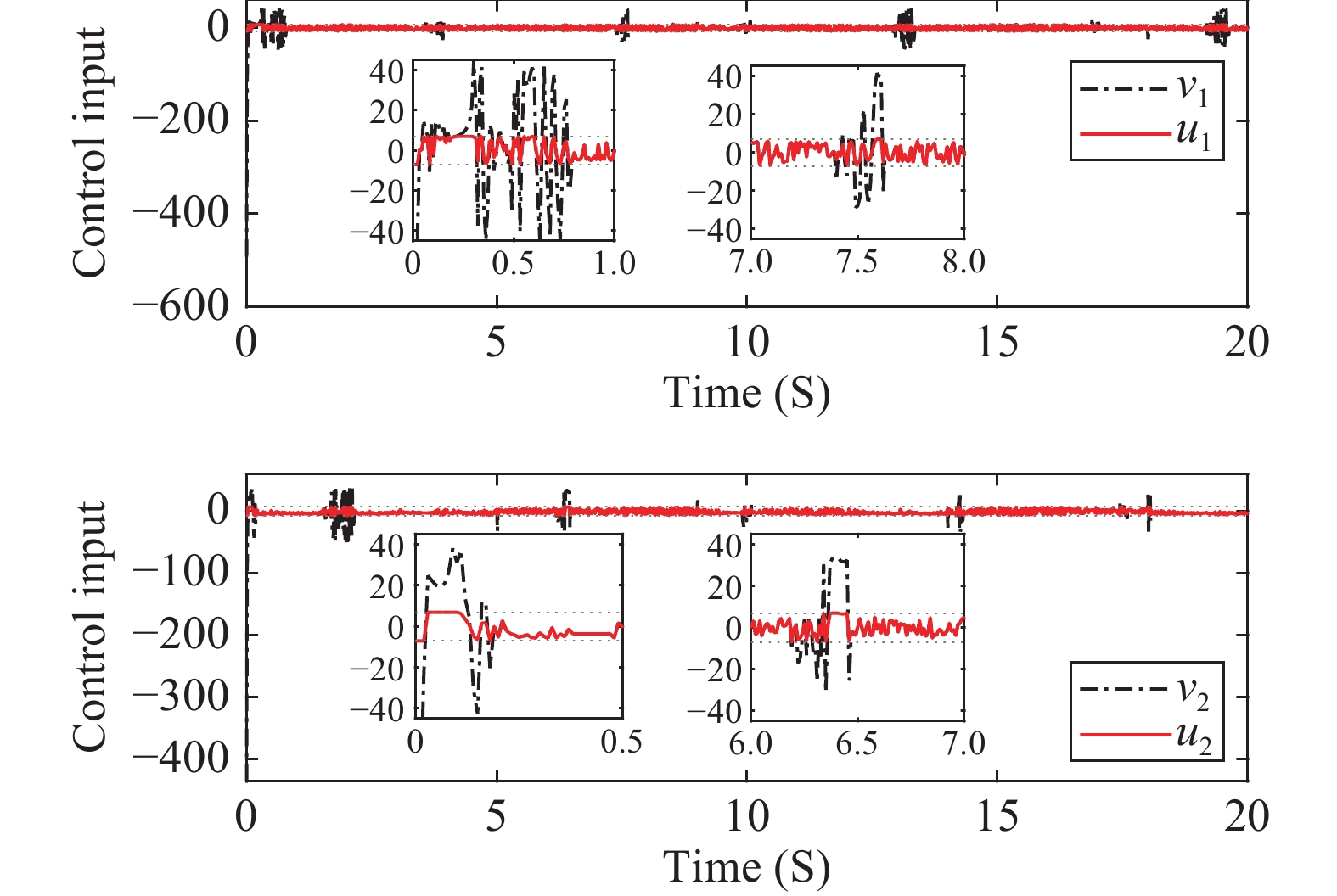
Figure 4. Example 1: Trajectories of the saturation input and
and .
.

Figure 5. Example 1: Trajectories of the tracking errors and
and based on the different settling time.
based on the different settling time.

Figure 6. Example 1: Trajectories of the filtering errors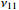 and
and based on the different settling time.
based on the different settling time.
Remark 9. It is seen in Figures 1 and 4 that, achieving fast convergence at the same time implies that the control input needs to be large enough. Therefore, the trade-off between better tracking performance and less control energy is a constant consideration for researchers, where the consideration of the input saturation in system (14) can be treated as a reasonable solution. However, as shown from Figures 4 and 9, the obvious deficiency is that, the control input results are not smooth enough due to switching. Theoretically, the term is similar to the sign function if is too small, which obviously results in the chattering phenomenon.
Example 2: To further demonstrate the feasibility and effectiveness of the proposed scheme in this article, we consider a practically predefined-time control problem [49] of a permanent magnet synchronous motor model with a smooth air gap.
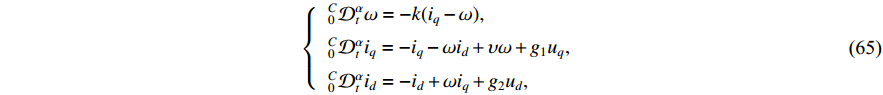
where 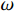 ,
,  and
and 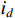 stand for the rotor angular velocity, the current of the
stand for the rotor angular velocity, the current of the  axis and the current of the
axis and the current of the  axis, respectively.
axis, respectively. 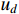 and
and  denote the
denote the 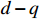 axis voltage. Assume that only two controllers
axis voltage. Assume that only two controllers 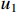 and
and  are applied to system (65). The system parameters are set as
are applied to system (65). The system parameters are set as  ,
,  ,
, 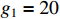 and
and 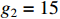 . In this simulation, we denote
. In this simulation, we denote  ,
,  and
and  . Then, the fractional-order dynamic equation of this mechanical system can be transformed to a typical form (64) where
. Then, the fractional-order dynamic equation of this mechanical system can be transformed to a typical form (64) where 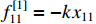 ,
, 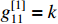 ,
,  ,
,  ,
,  ,
, 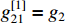 ,
,  ,
, 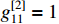 ,
,  ,
,  ,
, 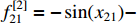 , and
, and 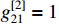 .
.
The fractional order is selected as 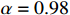 and the reference signals are assumed to be
and the reference signals are assumed to be 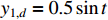 and
and  . The design parameters of this example are chosen as
. The design parameters of this example are chosen as  ,
, 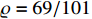 ,
, 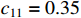 ,
, 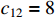 ,
,  ,
,  ,
, 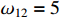 and
and  . Other parameters are selected the same with Example 1.
. Other parameters are selected the same with Example 1.
Figures 7−11 depict the corresponding simulation results. The qualitative analysis results of this example are identical to that of Example 1. From these figures, we can observe that the tracking error of the presented method can be tuned to a smaller neighborhood of the origin. Moreover, the given upper boundary on the settling-time provides the user with more practical metrics to understand and tune the system performance.
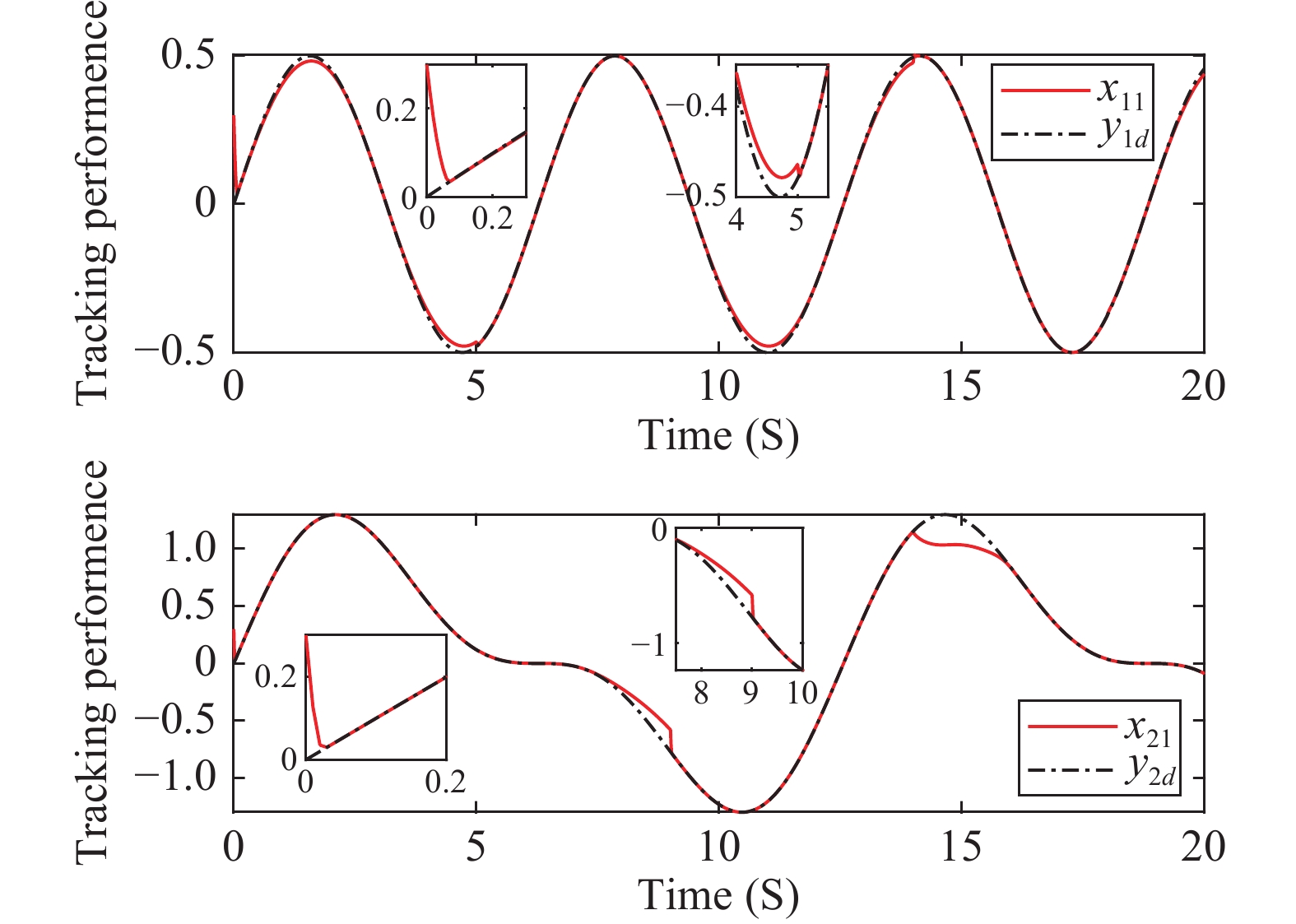
Figure 7. Example 2: Trajectories of system output and the reference signal
and the reference signal ,
, = 1, 2.
= 1, 2.

Figure 8. Example 2: Trajectories of the adaptive parameters and
and (
( =1, 2;
=1, 2; =1, 2).
=1, 2).

Figure 9. Example 2: Trajectories of the saturation input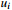 and
and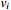 .
.

Figure 10. Example 2: Trajectories of the tracking errors and
and based on the different settling time.
based on the different settling time.
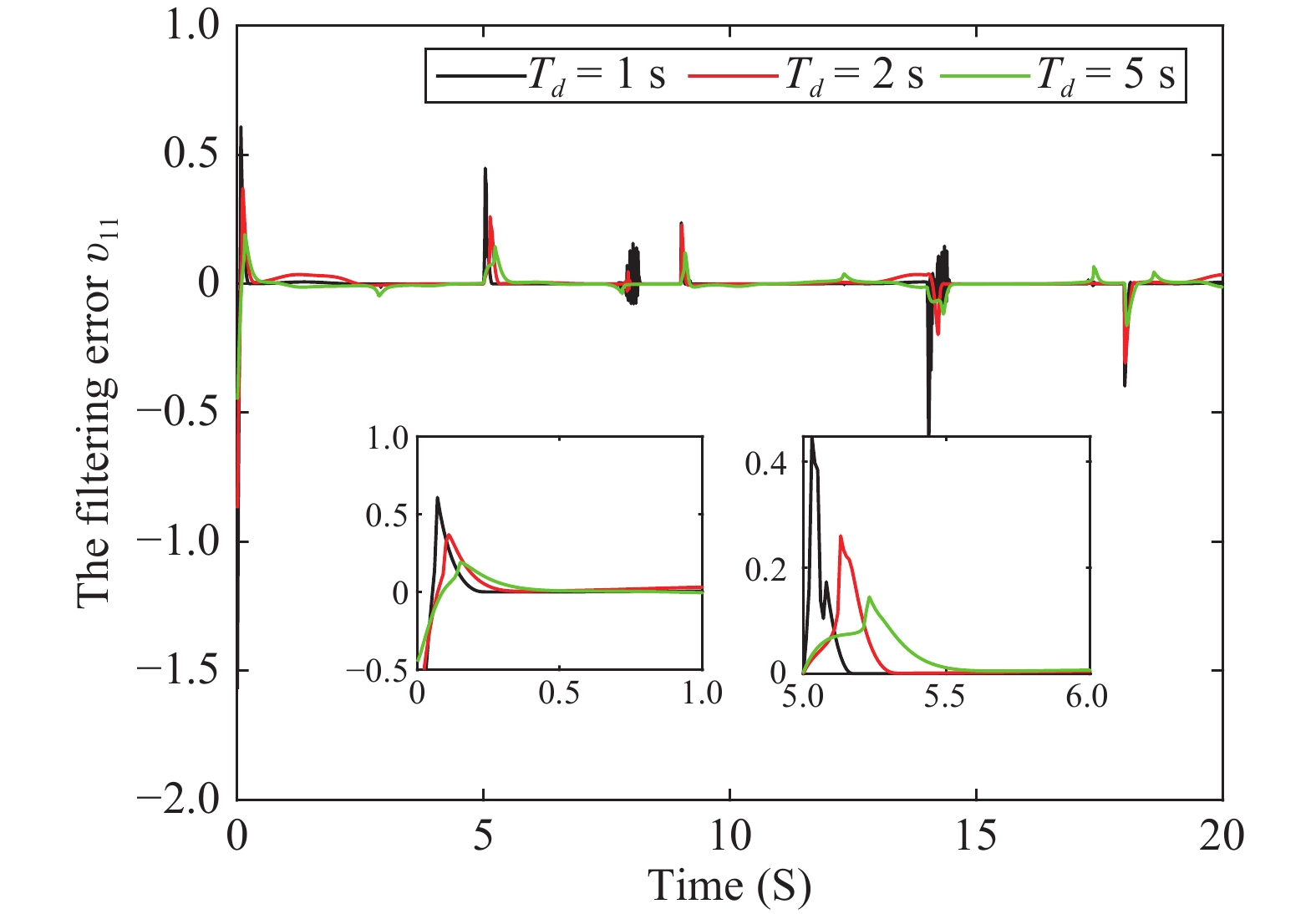
Figure 11. Example 2: Trajectories of the filtering errors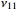 based on the different settling time.
based on the different settling time.
5. Conclusion
In this article, the fuzzy adaptive predefined-time tracking control problem has been investigated for a class of switched fractional-order nonlinear systems in the presence of input saturation and external disturbances. A new predefined-time auxiliary function has been constructed to guarantee the convergence of the tracking error to a bounded compact set within a user-defined time. Furthermore, to deal with the complex calculation problem and the singularity problem, a novel predefined-time filter has been designed in the design process of an adaptive controller in order to obtain better tracking performance. In the end, the simulations have been provided to show the effectiveness of the proposed method. In the future, we will extend the proposed approach to deal with the practical prescribed-time convergence problem of the fractional-order nonlinear systems subject to cyber-attacks.
Author Contributions: All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Lusong Ding and Weiwei Sun. The first draft of the manuscript was written by Lusong Ding and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding: This work was supported in part by the National Natural Science Foundation of China under Grant 62073189 and Grant 62173207, in part by the Taishan Scholar Project of Shandong Province under Grant tsqn 202211129.
Conflicts of Interest: The authors declare no conflict of interest.
References
- Bataghva, M.; Hashemi, M. Adaptive sliding mode synchronisation for fractional-order non-linear systems in the presence of time-varying actuator faults.
IET Control Theory Appl . 2018,12 , 377–383. DOI: https://doi.org/10.1049/iet-cta.2017.0458 - Aghababa, M.P. Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int. J. Control, 2013, 86: 1744−1756. doi: 10.1080/00207179.2013.796068 DOI: https://doi.org/10.1080/00207179.2013.796068
- Nikdel, N.; Badamchizadeh, M.; Azimirad, V.; et al. Fractional-order adaptive backstepping control of robotic manipulators in the presence of model uncertainties and external disturbances. IEEE Trans. Ind. Electron., 2016, 63: 6249−6256. doi: 10.1109/TIE.2016.2577624 DOI: https://doi.org/10.1109/TIE.2016.2577624
- Ma, Z.Y.; Ma, H.J. Adaptive fuzzy backstepping dynamic surface control of strict-feedback fractional-order uncertain nonlinear systems. IEEE Trans. Fuzzy Syst., 2020, 28: 122−133. doi: 10.1109/TFUZZ.2019.2900602 DOI: https://doi.org/10.1109/TFUZZ.2019.2900602
- Liu, H.; Pan, Y.P.; Li, S.G.; et al. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst., 2017, 47: 2209−2217. doi: 10.1109/TSMC.2016.2640950 DOI: https://doi.org/10.1109/TSMC.2016.2640950
- Jafari, A.A.; Mohammadi, S.M.A.; Farsangi, M.M.; et al. Observer-based fractional-order adaptive type-2 fuzzy backstepping control of uncertain nonlinear MIMO systems with unknown dead-zone. Nonlinear Dyn., 2019, 95: 3249−3274. doi: 10.1007/s11071-018-04754-0 DOI: https://doi.org/10.1007/s11071-018-04754-0
- Zhan, Y.L.; Li, X.M.; Tong, S.C. Observer-based decentralized control for non-strict-feedback fractional-order nonlinear large-scale systems with unknown dead zones. IEEE Trans. Neural Netw. Learn. Syst., 2023, 34: 7479−7490. doi: 10.1109/TNNLS.2022.3143901 DOI: https://doi.org/10.1109/TNNLS.2022.3143901
- Gong, P.; Lan, W.Y. Adaptive robust tracking control for multiple unknown fractional-order nonlinear systems. IEEE Trans. Cybern., 2019, 49: 1365−1376. doi: 10.1109/TCYB.2018.2801345 DOI: https://doi.org/10.1109/TCYB.2018.2801345
- Sun, W.W.; Wang, L.P.; Wu, Y. Adaptive dynamic surface fuzzy control for state constrained time-delay nonlinear nonstrict feedback systems with unknown control directions. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 7423−7434. doi: 10.1109/TSMC.2020.2969289 DOI: https://doi.org/10.1109/TSMC.2020.2969289
- Sun, W.W.; Wu, Y.; Lv, X.Y. Adaptive neural network control for full-state constrained robotic manipulator with actuator saturation and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst., 2022, 33: 3331−3342. doi: 10.1109/TNNLS.2021.3051946 DOI: https://doi.org/10.1109/TNNLS.2021.3051946
- Ding, D.R.; Wang, Z.D.; Han, Q.L. Neural-network-based consensus control for multiagent systems with input constraints: The event-triggered case. IEEE Trans. Cybern., 2020, 50: 3719−3730. doi: 10.1109/TCYB.2019.2927471 DOI: https://doi.org/10.1109/TCYB.2019.2927471
- Wen, C.Y.; Zhou, J.; Liu, Z.T.; et al. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Automat. Control, 2011, 56: 1672−1678. doi: 10.1109/TAC.2011.2122730 DOI: https://doi.org/10.1109/TAC.2011.2122730
- Chen, M.; Ge, S.S.; Ren, B.B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica, 2011, 47: 452−465. doi: 10.1016/j.automatica.2011.01.025 DOI: https://doi.org/10.1016/j.automatica.2011.01.025
- Song, S.; Zhang, B.Y.; Song, X.N.; et al. Neuro-fuzzy-based adaptive dynamic surface control for fractional-order nonlinear strict-feedback systems with input constraint. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 3575−3586. doi: 10.1109/TSMC.2019.2933359 DOI: https://doi.org/10.1109/TSMC.2019.2933359
- Wang, C.H.; Cui, L.M.; Liang, M.; et al. Adaptive neural network control for a class of fractional-order nonstrict-feedback nonlinear systems with full-state constraints and input saturation. IEEE Trans. Neural Netw. Learn. Syst., 2022, 33: 6677−6689. doi: 10.1109/TNNLS.2021.3082984 DOI: https://doi.org/10.1109/TNNLS.2021.3082984
- Cao, B.Q.; Nie, X.B. Event-triggered adaptive neural networks control for fractional-order nonstrict-feedback nonlinear systems with unmodeled dynamics and input saturation. Neural Netw., 2021, 142: 288−302. doi: 10.1016/j.neunet.2021.05.014 DOI: https://doi.org/10.1016/j.neunet.2021.05.014
- Zeng, D.P.; Liu, Z.; Chen, C.L.P.; et al. Event-triggered fuzzy adaptive control of nonlinear switched systems with predefined accuracy and mismatched switching. Fuzzy Sets Syst., 2022, 443: 283−307. doi: 10.1016/j.fss.2021.10.004 DOI: https://doi.org/10.1016/j.fss.2021.10.004
- Geng, H.; Wang, Z.D.; Yi, X.J.; et al. Tobit Kalman filtering for fractional-order systems with stochastic nonlinearities under round-robin protocol. Int. J. Robust Nonlinear Control, 2021, 31: 2348−2370. doi: 10.1002/rnc.5396 DOI: https://doi.org/10.1002/rnc.5396
- Sisbot, E.A.; Marin-Urias, L.F.; Alami, R.; et al. A human aware mobile robot motion planner. IEEE Trans. Robot., 2007, 23: 874−883. doi: 10.1109/TRO.2007.904911 DOI: https://doi.org/10.1109/TRO.2007.904911
- Shi, K.B.; Wang, J.; Zhong, S.M.; et al. New reliable nonuniform sampling control for uncertain chaotic neural networks under Markov switching topologies. Appl. Math. Comput., 2019, 347: 169−193. doi: 10.1016/j.amc.2018.11.011 DOI: https://doi.org/10.1016/j.amc.2018.11.011
- Ma, R.C.; Zhao, J. Backstepping design for global stabilization of switched nonlinear systems in lower triangular form under arbitrary switchings. Automatica, 2010, 46: 1819−1823. doi: 10.1016/j.automatica.2010.06.050 DOI: https://doi.org/10.1016/j.automatica.2010.06.050
- Long, L.J.; Zhao, J. Switched-observer-based adaptive neural control of MIMO switched nonlinear systems with unknown control gains. IEEE Trans. Neural Netw. Learn. Syst., 2017, 28: 1696−1709. doi: 10.1109/TNNLS.2016.2521425 DOI: https://doi.org/10.1109/TNNLS.2016.2521425
- Bi, W.S.; Wang, T.; Yu, X.H. Fuzzy adaptive decentralized control for nonstrict-feedback large-scale switched fractional-order nonlinear systems. IEEE Trans. Cybern., 2022, 52: 8887−8896. doi: 10.1109/TCYB.2021.3061136 DOI: https://doi.org/10.1109/TCYB.2021.3061136
- Sui, S.; Chen, C.L.P.; Tong, S.C. Neural-network-based adaptive DSC design for switched fractional-order nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst., 2021, 32: 4703−4712. doi: 10.1109/TNNLS.2020.3027339 DOI: https://doi.org/10.1109/TNNLS.2020.3027339
- Sui, S.; Tong, S.C. FTC design for switched fractional-order nonlinear systems: An application in a permanent magnet synchronous motor system. IEEE Trans. Cybern., 2023, 53: 2506−2515. doi: 10.1109/TCYB.2021.3123377 DOI: https://doi.org/10.1109/TCYB.2021.3123377
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim., 2000, 38: 751−766. doi: 10.1137/S0363012997321358 DOI: https://doi.org/10.1137/S0363012997321358
- Li, H.L.; Hu, C.; Zhang, L.; et al. Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control. Fuzzy Sets Syst., 2022, 443: 50−69. doi: 10.1016/j.fss.2021.11.004 DOI: https://doi.org/10.1016/j.fss.2021.11.004
- Bigdeli, N.; Ziazi, H.A. Finite-time fractional-order adaptive intelligent backstepping sliding mode control of uncertain fractional-order chaotic systems. J. Franklin Inst., 2017, 354: 160−183. doi: 10.1016/j.jfranklin.2016.10.004 DOI: https://doi.org/10.1016/j.jfranklin.2016.10.004
- Kamal, S.; Raman, A.; Bandyopadhyay, B. Finite-time stabilization of fractional order uncertain chain of integrator: An integral sliding mode approach. IEEE Trans. Automat. Control, 2013, 58: 1597−1602. doi: 10.1109/TAC.2012.2228051 DOI: https://doi.org/10.1109/TAC.2012.2228051
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Automat. Control, 2012, 57: 2106−2110. doi: 10.1109/TAC.2011.2179869 DOI: https://doi.org/10.1109/TAC.2011.2179869
- Sun, Y.M.; Zhang, L. Fixed-time adaptive fuzzy control for uncertain strict feedback switched systems. Inf. Sci., 2021, 546: 742−752. doi: 10.1016/j.ins.2020.08.059 DOI: https://doi.org/10.1016/j.ins.2020.08.059
- Balamash, A.S.; Bettayeb, M.; Djennoune, S.; et al. Fixed-time terminal synergetic observer for synchronization of fractional-order chaotic systems. Chaos, 2020, 30: 073124. doi: 10.1063/1.5142989 DOI: https://doi.org/10.1063/1.5142989
- Jiménez-Rodríguez, E.; Munoz-Vazquez, A.J.; Sanchez-Torres, J.D.; et al. A Lyapunov-like characterization of predefined-time stability. IEEE Trans. Automat. Control, 2020, 65: 4922−4927. doi: 10.1109/TAC.2020.2967555 DOI: https://doi.org/10.1109/TAC.2020.2967555
- Munoz-Vazquez, A.J.; Sánchez-Torres, J.D.; Jiménez-Rodríguez, E.;
et al . Predefined-time robust stabilization of robotic manipulators.IEEE /ASME Trans. Mechatron .2019 ,24 , 1033–1040. - Zhang, T.L.; Bai, R.; Li, Y.M. Practically predefined-time adaptive fuzzy quantized control for nonlinear stochastic systems with actuator dead zone. IEEE Trans. Fuzzy Syst., 2023, 31: 1240−1253. doi: 10.1109/TFUZZ.2022.3197970 DOI: https://doi.org/10.1109/TFUZZ.2022.3197970
- Wang, Q.; Cao, J.D.; Liu, H. Adaptive fuzzy control of nonlinear systems with predefined time and accuracy. IEEE Trans. Fuzzy Syst., 2022, 30: 5152−5165. doi: 10.1109/TFUZZ.2022.3169852 DOI: https://doi.org/10.1109/TFUZZ.2022.3169852
- Yang, T.T.; Dong, J.X. Predefined-time adaptive fault-tolerant control for switched odd-rational-power multi-agent systems. IEEE Trans. Autom. Sci. Eng., 2023, 20: 2423−2434. doi: 10.1109/TASE.2022.3208029 DOI: https://doi.org/10.1109/TASE.2022.3208029
- Xu, H.; Yu, D.X.; Sui, S.; et al. An event-triggered predefined time decentralized output feedback fuzzy adaptive control method for interconnected systems. IEEE Trans. Fuzzy Syst., 2023, 31: 631−644. doi: 10.1109/TFUZZ.2022.3184834 DOI: https://doi.org/10.1109/TFUZZ.2022.3184834
- Yu, Z.L.; Li, Y.H.; Lv, M.L.; et al. Predefined-time anti-saturation fault-tolerant attitude control for tailless aircraft with guaranteed output constraints. Nonlinear Dyn., 2023, 111: 1399−1416. doi: 10.1007/s11071-022-07904-7 DOI: https://doi.org/10.1007/s11071-022-07904-7
- Xu, K.T.; Ge, M.F.; Liang, C.D.; et al. Predefined-time time-varying formation control of networked autonomous surface vehicles: A velocity- and model-free approach. Nonlinear Dyn., 2022, 108: 3605−3622. doi: 10.1007/s11071-022-07415-5 DOI: https://doi.org/10.1007/s11071-022-07415-5
- Xie, S.Z.; Chen, Q.; He, X.X. Predefined-time approximation-free attitude constraint control of rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst., 2023, 59: 347−358. doi: 10.1109/TAES.2022.3183550 DOI: https://doi.org/10.1109/TAES.2022.3183550
- Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M.; et al. Predefined-time convergence in fractional-order systems. Chaos Solitons Fractals, 2021, 143: 110571. doi: 10.1016/j.chaos.2020.110571 DOI: https://doi.org/10.1016/j.chaos.2020.110571
- Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M. Second-order predefined-time sliding-mode control of fractional-order systems. Asian J. Control, 2022, 24: 74−82. doi: 10.1002/asjc.2447 DOI: https://doi.org/10.1002/asjc.2447
- Cui, M.Y.; Tong, S.C. Event-triggered predefined-time output feedback control for fractional-order nonlinear systems with input saturation.
IEEE Trans. Fuzzy Syst .2023 , in press. DOI: https://doi.org/10.1109/TFUZZ.2023.3283783 - Podlubny, I.
Fractional Di fferential Equations ; Academic Press: San Diego, CA, USA, 1999. - Li, C.P.; Deng, W.H. Remarks on fractional derivatives. Appl. Math. Comput., 2007, 187: 777−784. doi: 10.1016/j.amc.2006.08.163 DOI: https://doi.org/10.1016/j.amc.2006.08.163
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul., 2014, 19: 2951−2957. doi: 10.1016/j.cnsns.2014.01.022 DOI: https://doi.org/10.1016/j.cnsns.2014.01.022
- Wang, L.X.; Mendel, J.M. Fuzzy basis functions, universal approximation, and orthogonal least-squares learning. IEEE Trans. Neural Netw., 1992, 3: 807−814. doi: 10.1109/72.159070 DOI: https://doi.org/10.1109/72.159070
- Mani, P.; Rajan, R.; Shanmugam, L.; et al. Adaptive fractional fuzzy integral sliding mode control for PMSM model. IEEE Trans. Fuzzy Syst., 2019, 27: 1674−1686. doi: 10.1109/TFUZZ.2018.2886169 DOI: https://doi.org/10.1109/TFUZZ.2018.2886169





