A Survey of Algorithms, Applications and Trends for Particle Swarm Optimization

2.1. The Original PSO Algorithm

Survey/review study

A Survey of Algorithms, Applications and Trends for Particle Swarm Optimization

Jingzhong Fang ¹, Weibo Liu ^1,*, Linwei Chen ², Stanislao Lauria ¹, Alina Miron ¹, and Xiaohui Liu ¹

¹ Department of Computer Science, Brunel University London, Uxbridge, Middlesex, UB8 3PH, United Kingdom

² The School of Engineering, University of Warwick, Coventry CV4 7AL, United Kingdom

^* Correspondence: Weibo.Liu2@brunel.ac.uk

Received: 18 October 2022

Accepted: 28 November 2022

Published: 27 March 2023

Abstract: Particle swarm optimization (PSO) is a popular heuristic method, which is capable of effectively dealing with various optimization problems. A detailed overview of the original PSO and some PSO variant algorithms is presented in this paper. An up-to-date review is provided on the development of PSO variants, which include four types i.e., the adjustment of control parameters, the newly-designed updating strategies, the topological structures, and the hybridization with other optimization algorithms. A general overview of some selected applications (e.g., robotics, energy systems, power systems, and data analytics) of the PSO algorithms is also given. In this paper, some possible future research topics of the PSO algorithms are also introduced.

1. Introduction

Optimization plays a critical role in a variety of research fields such as mathematics, economics, engineering, and computer science. Recognizing as a popular class of optimization techniques, the evolutionary computation (EC) methods have behaved competitive performance in effectively tackling optimization problems in an easy way. So far, the EC methods have been widely applied in numerous research fields thanks to their strong abilities in finding the optimal solutions [1]. Among the EC algorithms, some algorithms which are based on biological behaviours (e.g., the genetic algorithm (GA) [2], the ant colony optimization (ACO) algorithm [3] and the particle swarm optimization (PSO) algorithm [4,5]) have been well-adopted in a number of research areas e.g., energy systems, robotics, aerospace engineering and artificial intelligence.

As a population-based EC method, PSO is developed on the basis of the mimics of social behaviours e.g., the birds-flocking phenomenon and the fish-schooling phenomenon. Notably, the potential optimization solution is represented by a particle (also called as individual). During the searching process, each individual learns from the "movement experience" of itself and others. It should be mentioned that the advantages of PSO can be summarised into three aspects: (1) the number of parameters required to be adjusted is relatively few; (2) the convergence rate of the PSO algorithm is relatively fast; and (3) the implementation of the PSO algorithm is simple [6,7]. Owing to its technical merits and easy implementation, PSO has become a widely-used technique for tackling optimization problems in recent years [8-10].

Unfortunately, many population-based EC algorithms face the challenging problem that the potential solutions being easily trapped into the local optima especially under complex and high-dimensional scenarios. As a well-known EC algorithm, PSO is not an exception. As a result, developing new PSO methods has become a seemingly reasonable way to deal with the premature convergence puzzle [11-16]. For example, a group of PSO variants have been put forward by modifying the parameters [13-15]. In [14, 15], a linear decreasing mechanism has been proposed to alter the inertia weight, leading to a proper balance between the global discovery and the local detection. In [13], a novel optimizer has been introduced by presenting a time-varying strategy to adjust the acceleration coefficients, which enhances the global search and convergence performance.

Apart from modifying the control parameters, designing novel updating strategies has become a hot research direction in developing advanced PSO algorithms [17-21]. In particular, a powerful family of improved optimizers has been proposed by embedding the switching strategy into the velocity model, thereby improving the optimal solution discovery of PSO [18,21-23]. In [21], an evolutionary factor has been designed for updating control parameters, which divides the evolution process into four different states. In [18], a switching scheme has been embedded into PSO depending on the Markov chain (which is used to determine the evolutionary states) with the aim of improving the convergence of the optimizer.

The neighbourhood information of each individual is of practical significance in finding the optimal solution. Recently, various topological structures have been designed to comprehensively utilize the neighbourhood information of each individual so as to carry out a thorough exploration in the problem space [16,24]. In [16], a variable neighbourhood operator has been introduced for improving the optimizer's search ability. A dynamically adjusted neighbourhood has been designed in [24] to enhance the information sharing in the swarm.

Hybridizing PSO with other EC algorithms is also a well-known technique in designing new PSO methods [12, 25]. For instance, in [26], the PSO algorithm has been hybridized with differential evolution to: (1) enhance the current local best particles' search strategy; and (2) enhance the possibility of individuals slipping away from the local optima. A mutation operator has been embedded into the PSO algorithm [25], which improves the convergence rate and expands the search space.

Owing to their relatively fast convergence rate and satisfactory solution quality, the PSO algorithms have been successfully applied to robot path planning, machine allocation, transportation, electricity trading, etc [27-30]. In [27], PSO has been adopted to handle the mobile robot path planning problem. A PSO-based detection approach has been put forward in [8] for finding the maximum power point in the energy power system. An improved PSO method has been developed in [30] with the purpose of handling the economic dispatch challenge in the power system by incorporating the constriction factor. A PSO-based trajectory planning approach has been introduced in [29] to find the optimal trajectory of the spacecraft. PSO has also been adopted to tackle the centroid location optimization in K-means clustering [31].

This paper aims to deliver a comprehensive and timely review of the PSO algorithms and their applications. An up-to-date review of some PSO variants is also introduced. In this paper, PSO applications in several areas are discussed. In Section 2, details of original PSO as well as basic PSO are presented. In Section 3, some existing "variant PSO algorithms" including the latest development of PSO algorithms are summarized. In Section 4, some popular practical applications of PSO algorithms are pointed out. Some possible future research topics are listed in Section 5. The conclusion is given in Section 6.

2. The PSO Algorithms

Original PSO is a prominent EC algorithm, which aims to discover the global optimum in the problem space by tuning the velocity and position of the particles [4,5]. Basically, each element of the swarm is an individual particle serving as a candidate solution. The movement of each particle is guided by (1) its previous "flying experience" which is the personal best location (i.e., pbest); and (2) the "group flying experience" which is the global best location (i.e., gbest) detected by the entire swarm.

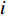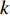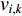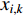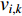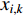All the individuals search the problem space which has dimensions to seek the optimal solution. The velocity and position of the  th particle at the th iteration are denoted by  and , respectively. At the beginning,  and  are randomly initialized. During the evolution process, the velocity and position updating equations of the  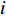th particle are given as follows:

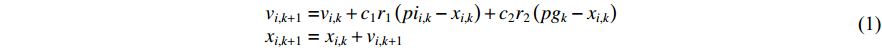
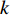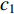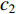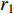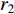where  denotes the iteration number;  is an acceleration factor named the cognitive parameter;  is the social acceleration parameter;  and  are two separate random numbers selected within 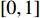;  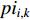represents the personal best location found by the 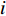th particle itself, which is denoted by 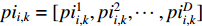;  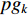represents the global best location of all the particles, which is denoted by 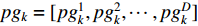.  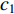and 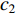 indicate the degree of each particle affected by itself and other particles, respectively [32]. The acceleration coefficients play an important role in balancing the local discovery and global search performance, and also have significant influence on the population diversity, solution quality, and convergence behavior of the algorithm.

2.2. The Basic PSO Algorithm

Original PSO has shown strong abilities in solving optimization problems. Nevertheless, the particles may be easily trapped in the local optimal solutions. To guarantee the search performance and balance the global detection and local discovery, the inertia weight 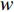 has been introduced in [33] as an important factor to improve the PSO algorithm, and such a factor indicates the ability of particles to inherit their previous velocities. The inertia weight embedded PSO algorithm has been recognized as the basic PSO algorithm. The velocity as well as the position of the 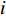th particle at the ( 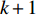)th iteration are expressed as follows:

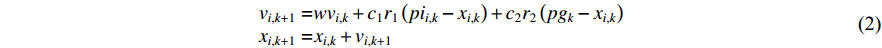
where 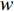 indicates the inertia weight. The basic PSO process is presented in Algorithm 1.

Algorithm 1 The Procedure of the Standard PSO Algorithm
1: Initialize the parameters of the PSO algorithm including the population size P, inertia weight w, acceleration coefficients c1, c2, and maximum velocity Vmax
2: Set a swarm that has P particles
3: Initialize the position xi,1 and the velocity vi,1, and pii,1 of each particle (i = 1,2,...,P); and initialize pg1 of the swarm
4: Calculate each particle’s fitness value
5: Update the pii,k of each particle and pgk of the swarm
6: Update the velocity vi,k and the position xi,k of each particle based on Equation (2)
7: Confirm whether the maximum iterations are met or the fitness value reaches the threshold, if not, go to step 4

3. Developments of the PSO Algorithm

Similar to most population-based EC algorithms, the PSO algorithm also faces the premature convergence problem [34]. In this case, it is of practical importance to put forward new PSO algorithms especially for solving large-scale optimization problems and multi-modal optimization problems. In this paper, the reviewed PSO variants can be categorized into four groups: (1) adjusting the control parameters; (2) developing new updating strategies; (3) designing various topological structures; and (4) combining with other EC algorithms. In this section, the aforementioned four types of PSO variants are reviewed and summarized.

3.1. Adjusting Control Parameters

In the PSO algorithm, the control parameters refer to the inertia weight and the acceleration factors, which are of practical significance in maintaining the balance between global discovery and local detection. In the past few decades, plenty of work has been conducted to adjust these control parameters for improving PSO. Some selected PSO variants with modified control parameters are reviewed and summarized in Figure 1.

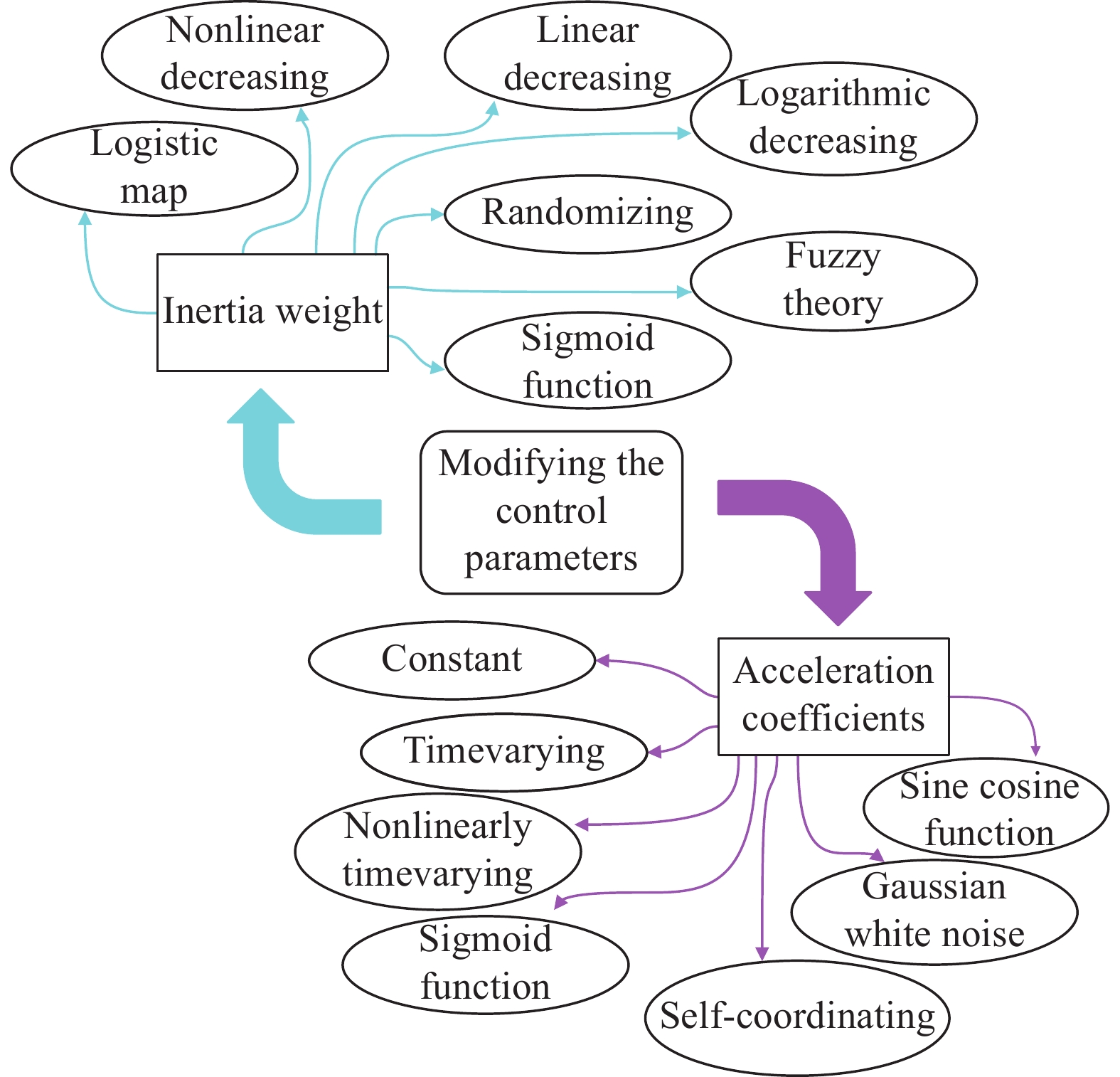
Figure 1. PSO variants with modified control parameters.

3.1.1. Inertia Weight

As an important parameter, the inertia weight is designed to achieve a proper balance between global discovery and local detection. A brief introduction is presented in Table 1 on the recently developed inertia-weight-based PSO variants.

Table 1. Inertia Weight Updating Strategies

Approach	Abbreviated Name	Reference
Linear Decreasing	Li-DIW	[14, 15]
	MIW-LD	[36]
	CLi-DIW	[44]
Non-linear Decreasing	NLFDIW	[37]
Sigmoid Function Based	SDIW	[38]
	SIIW	[39]
Logarithmic Decreasing	Lo-DIW	[40]
Randomizing	RIW	[41]
SA Algorithm Based	SAIW	[42]
Fuzzy Theory	FAPSO	[45]
Logistic Map Based	CDIW	[43]
	CRIW	[43]

It is known that a smaller inertia weight could lead to a better local search, while a larger inertia weight could contribute to a better global discovery [15]. The particles with satisfactory search ability would thoroughly exploit the solution space at the early step of search and avoid trapping into the local optima with high possibility. Additionally, the inertia weight would greatly affect the search ability of the particles. In [14, 15], starting from a relatively large value, the inertia weight is deployed to guarantee the global exploration performance. Then, the inertia weight is adjusted following the linear-decreasing strategy during the searching process with hope to enhance the local exploration. PSO with the linear decreasing inertia weight (Li-DIW) strategy has been proposed in [14, 15] where the inertia weight ( 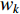) is updated as follows:

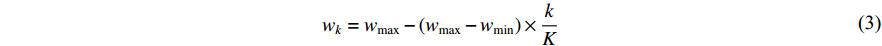
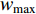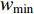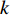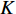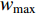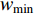where  and  denote the maximal and minimal inertia weight, respectively;  is the number of the current iteration; and  denotes the number of the maximum iteration during the evolution process. In [35],  and  are set to be  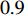and 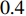, respectively, which becomes a normal setting in later development of PSO. The Li-DIW strategy has been widely used in developing various PSO algorithms.

It should be mentioned that a number of inertia weight updating strategies have been introduced based on the Li-DIW strategy. For example, a multi-stage inertia weight linearly decreasing strategy (MIW-LD) has been developed in [36] to better balance the global discovery and the local detection than the PSO with Li-DIW. The inertia weight ( 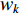) is updated by:

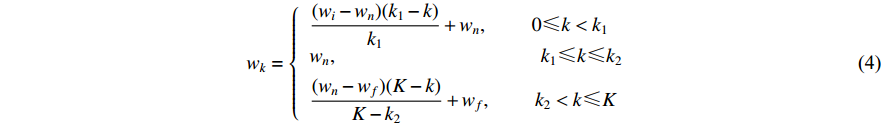
where 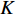 is the maximum iteration number;  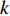is current iteration number;  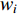and 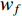 indicate the initial as well as the final value of the inertia weight, respectively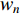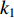; and ,  and 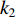 are the multi-stage parameters, which are manually selected based on experimental experience.

Different from the Li-DIW strategy, another inertia weight updating strategy is the nonlinear decreasing strategy. A nonlinear function modulated inertia weight (NLFDIW) has been developed in [37], and the updating equation of 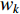 is presented as follows:

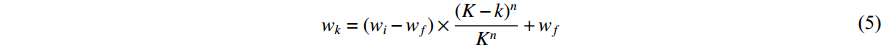
where 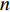 represents the nonlinear modulation index. The proposed NLFDIW could improve the convergence speed and tune the optimal solution detection strategy.

Another nonlinear function, the sigmoid function has been adopted in [38] to control the inertia weight, where a sigmoid-based decreasing inertia weight (SDIW) strategy is put forward to improve the convergence speed. The updating equation of the inertia weight ( 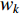) is given as:

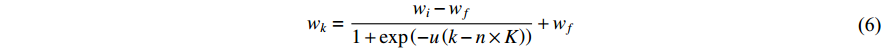
where 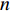 and 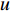 are constant values to set partition of the function and to adjust the sharpness of the function, respectively.

In [39], another sigmoid function modulated inertia weight has been introduced, which is called as the sigmoid-based increasing inertia weight (SIIW). The updating equation of the inertia weight ( 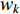) is shown below:

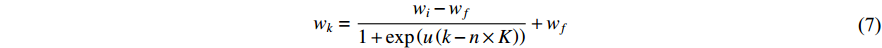
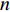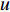where  and  are constants to set partition of the function and to alter the function sharpness, respectively. The SIIW exhibits faster convergence rate than standard PSO.

A logarithm decreasing inertia weight (Lo-DIW) strategy has been introduced in [40] to improve the convergence rate. The updating equation of the inertia weight ( 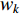) is shown below:

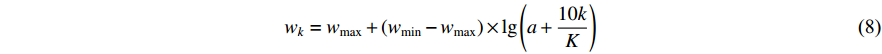
where 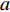 is a constant value for controlling the evolutionary speed.

The global search ability becomes weak when inertia weight decreases, and the particles may fall into the local optima [6]. In the past few decades, improving the search ability of PSO has been a hot research topic by changing the inertia weight in various aspects. It is found that the PSO algorithm with Li-DIW cannot obtain satisfactory results when dealing with a nonlinear dynamic system. In this case, the random inertia weight (RIW) scheme has been proposed in [41] for tracking and optimizing a dynamic system.

Some inertia weight updating strategies are designed by using other optimization algorithms. For example, in [42], the SA integrated inertia weight (SAIW) has been introduced, where 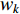 is updated as follows:

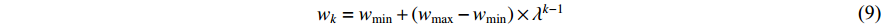
where 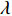 is a factor used to modify the temperature parameter of the SA algorithm, which is set to be 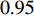. Comparing with the standard PSO, the SAIW-based PSO shows faster convergence speed.

Using the logistic map, the chaotic-descending-based inertia weight (CDIW) strategy and the chaotic-embedded random inertia weight (CRIW) strategy have been proposed in [43]. 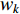 using the CDIW strategy is updated by:

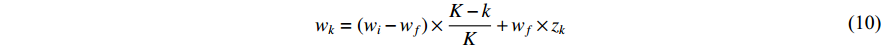
where 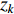 is the logistic map. The updating equation of inertia weight ( 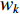) using the CRIW strategy is shown as follows:

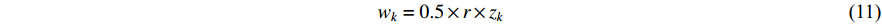
where 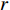 is a random number selected from 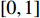; and 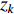 is the logistic map. Both CDIW and CRIW strategies improve the convergence rate, the convergence accuracy and the global discovery ability of PSO. Comparing with the RIW, the CRIW shows better convergence rate and solution accuracy.

In [44], the chaotic-embedded LD inertia weight (CLi-DIW) strategy has been proposed, which embeds the chaotic sequences into the Li-DIW strategy. The updating equation of the inertia weight ( 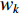) using the CLi-DIW strategy is given by:

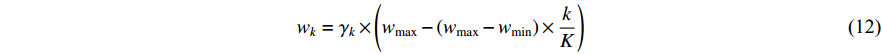
where 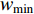 and 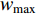 represent the minimal and maximal value of the inertia weight, respectively;  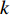and 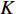 represent the current iteration number and the maximum iteration number, respectively; and  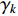is the chaotic parameter at the 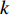th iteration. The CLi-DIW improves the particles' searching capability which could make it easier to slip away from the local optima.

In recent years, the fuzzy theory has been successfully applied to the PSO algorithm [45]. A fuzzy system based PSO algorithm (FAPSO) has been designed in [45], where the inputs of the fuzzy-based method are the normalized current best performance evaluation (NCBPE) as well as the current inertia weight, and the output variable of the fuzzy system is the change of the inertia weight. NCBPE is used to evaluate the best candidate solution discovered by the PSO algorithm.

3.1.2. Acceleration Coefficients

In recent years, many PSO variants which focus on the modification of the acceleration coefficients have been introduced. The reviewed acceleration coefficient updating strategies are summarized in Table 2.

Table 2. Some Acceleration Coefficient Updating Strategies

Approach	Abbreviated Name	Reference
Constant	Constant AC	[46, 47]
Time-varying	TVAC-1	[13]
	TVAC-2	[49]
	ATVAC	[50]
Non-linear Time-varying	NDAC	[51]
	NTVAC	[52]
Sigmoid Function Based	SBAC	[53]
	AWAC	[54]
Sine Cosine Function Based	SCAC	[55]
Adding Gaussian White Noises	GWNAC	[56]
Self-coordinating	SAC	[57]

The effect of two acceleration coefficients on each particle's movement is illustrated in Figure 2. According to [5], a relatively larger cognitive component could make particles search in a wider space comparing with the social component. In the original PSO algorithm, the acceleration components are constant values which are set to be 2.

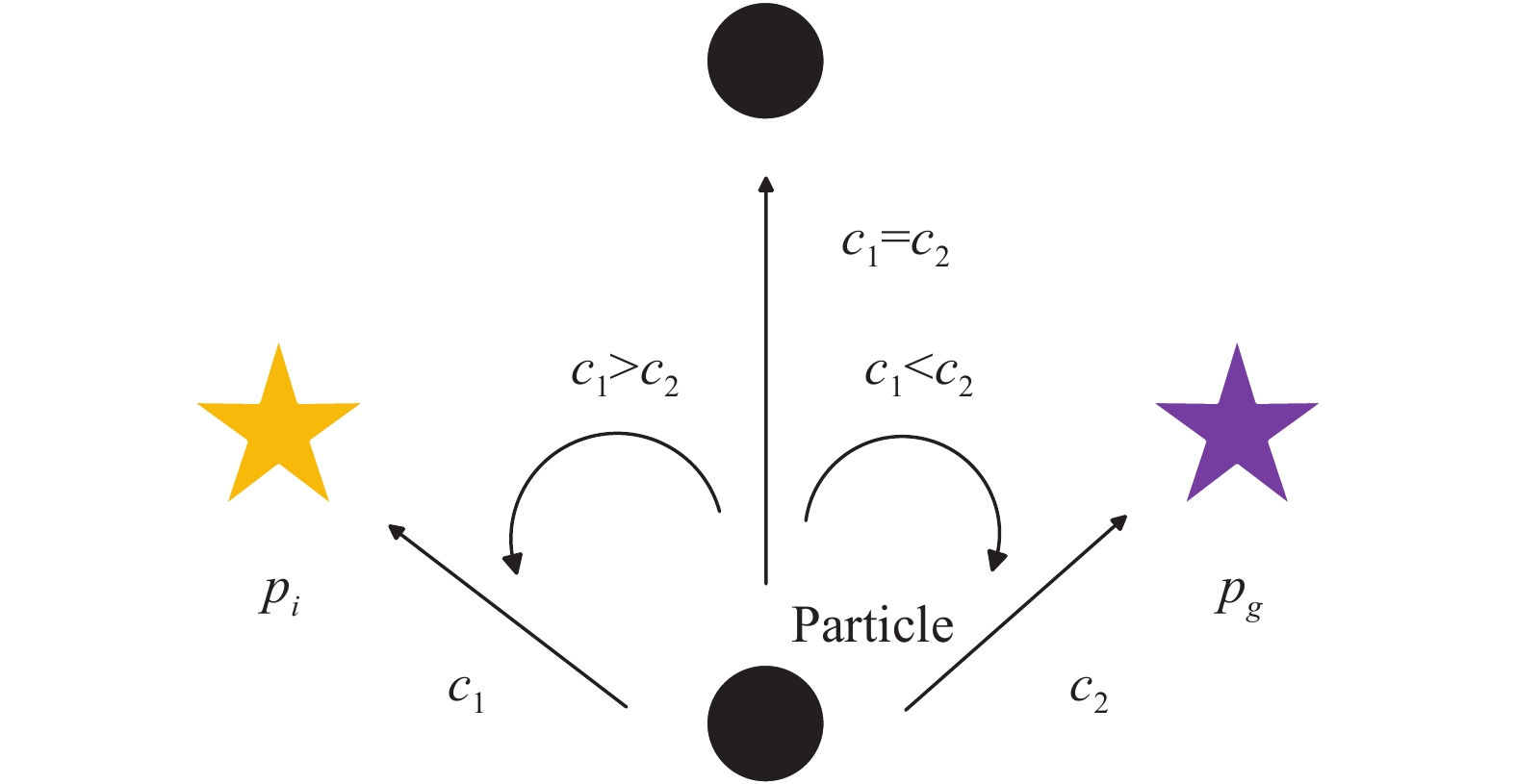
Figure 2. The effect of the value of the acceleration coefficients on the movement of the particle.

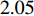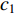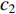A number of new PSO methods have been put forward where different acceleration factor updating strategies have been adopted for specific optimization problems. In [46], the acceleration coefficients are set to be  to guarantee the convergence of the optimizer. In [47],  and  are set to be  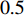and 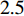, respectively.

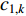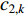It is worth noting that a relatively larger social component may easily lead to the premature convergence problem. The time-varying acceleration coefficient-embedded scheme (TVAC-1) has been proposed in [13], where the updating equations of the acceleration factors (  and ) are expressed as follows:

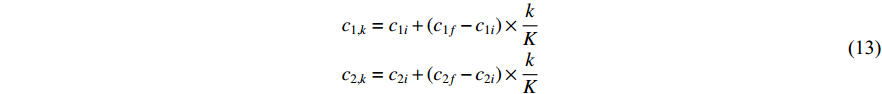
where 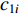 and 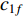 indicate the initial and final values of the cognitive component, respectively;  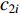and 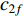 are the initial and final values of the social component, respectively;  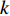is the current iteration number; and  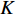is the maximum iteration number. The time-varying scheme for altering acceleration factors could not only improve the global discovery at the early step of the searching process, but also the convergence of particles towards the globally optimal solution at the latter step of the evolution process. According to the experimental results reported in [13], the parameters are set to be 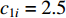, , 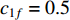, 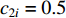and 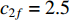. Based on the TVAC-1, a new updating strategy has been introduced to adjust the time-varying acceleration coefficients with unsymmetrical transfer range (UTRAC) in [48]. The UTRAC improves the convergence speed of the PSO algorithm.

In [49], another time-varying acceleration coefficients (TVAC-2) updating strategy has been proposed, which could further improve the solution accuracy. The updating equations of the acceleration coefficients ( 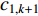 and 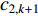) using the TVAC-2 strategy are given by:

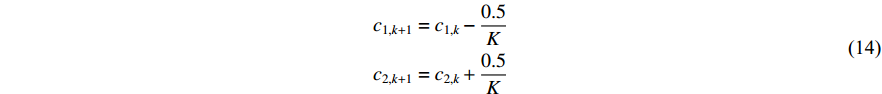
where 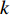 and 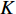 represent the current and the maximum iteration number, respectively.

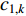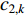The asymmetric time-varying-based strategy for controlling acceleration coefficients (ATVAC) has been proposed in [50], where the ATVAC demonstrates merits in balancing global and local search and improving the convergence as well as the robustness. In ATVAC, the updating formulas of  and  are expressed by:

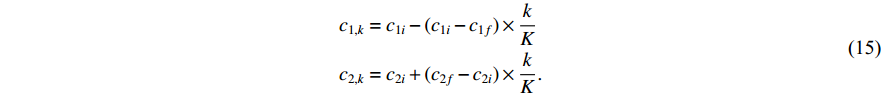
The nonlinear dynamic mechanism has been introduced in [51] to alter the acceleration factors. The updating equations of the nonlinear dynamic acceleration coefficients (NDAC) are expressed as follows:

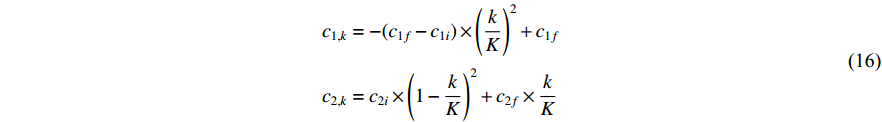
where 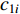 and 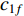 are the initial and final cognitive factors, respectively;  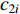and 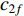 are the initial and final social acceleration factors, respectively;  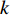is the current iteration number; and  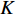is the maximum iteration number.

In [52], a set of non-linear time-varying acceleration coefficients (NTVAC) have been put forward to alleviate premature convergence. 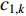 and 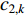 of the PSO algorithm with NTVAC are updated by:

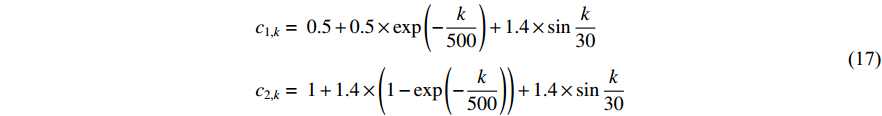
where 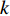 denotes the current iteration number.

As a popular nonlinear function, the sigmoid function has been used to adjust acceleration coefficients. In [53], sigmoid-function-based acceleration coefficients (SBAC) updating strategy has been proposed. The acceleration coefficients ( 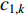 and 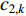) of the PSO algorithm with SBAC are updated by:

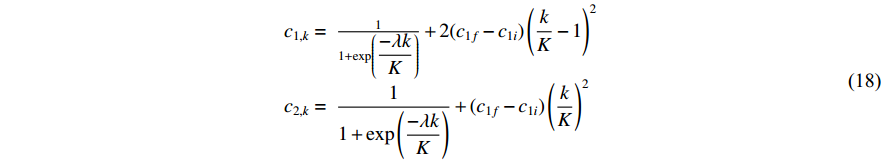
where 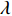 is a control parameter which is set to be .

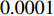In [54], a sigmoid-function-based adaptive weighted acceleration coefficients (AWAC) strategy has been developed, where an adaptive weighting updating function has been proposed by exploiting the distance from the particle to its pbest and gbest in order to adjust the acceleration coefficients. The updating equations of 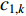 and 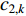 in the PSO algorithm with AWAC are expressed as follows:

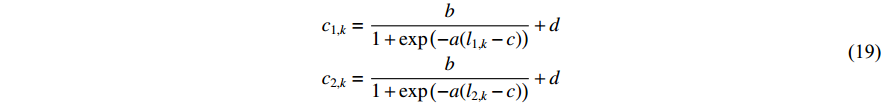
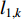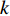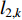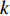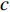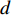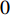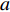where  denotes the distance from an individual to its pbest at the  th iteration;  denotes the distance between the individual and the gbest at the th iteration;  and  are two parameters which are set to be  and , respectively; and  and 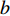 are two parameters used to describe the curve, which are set to be  and 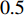, respectively. Note that  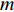is the range of search space of the problem.

The sine cosine acceleration coefficients (SCAC) updating strategy has been proposed in [55]. The updating equations of 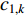 and 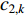 in the PSO algorithm with SCAC are given by:

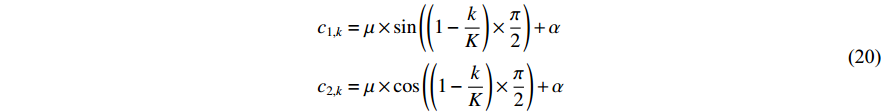
where 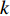 and 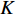 denote the current iteration number and the maximum iteration number, respectively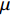; and  and 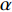 are two constants, which are set to be  and 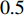, respectively. SCAC could not only motivate a thorough local detection but also force the candidates moving to the global optimal solution.

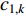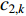Gaussian white noise-embedded acceleration coefficients (GWNAC) have been introduced in [56], where  and  are updated by:

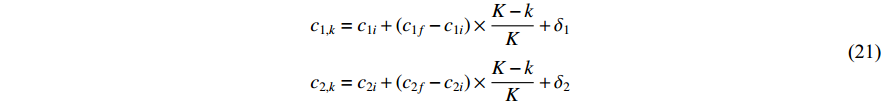
where 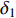 and 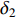 are two independent GWNs. By randomly perturbing the acceleration factors, the population diversity is maintained and the possibility of slipping away from the local optima is greatly enhanced.

In [57], a novel adaptive method has been proposed, where the acceleration factors are modified adaptively to make the target particle self-coordinates. The acceleration factors of the 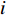th particle (  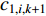and 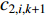) are updated by:

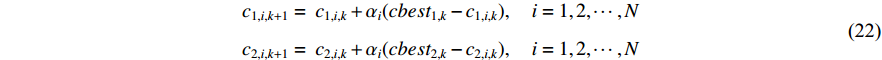
where 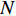 is the swarm size;  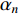represents the step size which is used to change the diversity of each particle; and  and  are the parameters which update the global best at certain iterations.

3.2. Developing Updating Strategies

Apart from adjusting control parameters of the PSO algorithm, many researchers have focused on designing new updating strategies of the PSO algorithm in the past few decades. The reviewed approaches on developing new algorithm updating strategies are summarized in Table 3.

Table 3. Developing New Algorithm Updating Strategies

Approach	Abbreviated Name	Reference
Re-initialization	VBRPSO	[59]
	RPSO	[17]
	RRPSO	[60]
	ERPSO	[60]
Switching Strategy	ARPSO	[61]
	APSO	[21]
	SPSO	[18]
	ISPSO	[62]
	SDPSO	[23]
	MDPSO	[63]
	ARFPSO	[64]
	DNSPSO	[24]
	RODDPSO	[22]
	FVSPSO	[66]
	SASPSO	[58]
Clustering Algorithm	CAPSO	[69]
Constriction Factor	CFPSO	[46, 70]
Comprehensive Learning	CLPSO	[34]
Multi-elitist Strategy	MEPSO	[73]
Fractional Velocity	FVPSO	[65]
FPGA Based	PMPSO	[27]
Detection Function Based	IDPSO	[74]
Quantum	QPSO	[75]
Cooperative	CPSO	[72]

3.2.1. Re-initialization

Re-initialization is a strategy which could help alleviate premature convergence [58]. In [59], a velocity-based re-initialization PSO (VBRPSO) algorithm has been presented to alleviate the premature convergence problem. In the VBRPSO algorithm, the particle velocity is monitored during the evolution process. If the median value of the norms of the velocity of the entire swarm is lower than a threshold, the swarm is treated to be stagnant and the algorithm will restart. More specifically, the stagnation can be determined by: (1) computing the Euclidean norm of the particle's velocity one by one; (2) sorting the obtained norms; and (3) comparing the median of the obtained norms with the pre-set threshold. If the median value of the norms is lower than the threshold, the swarm is stagnant.

In [17], an improved PSO algorithm with re-initialization mechanisms (RPSO) has been introduced, where the re-initialization process is determined based on the estimation of the varieties and activities of the particles. A new factor named "steplength" is employed to determine whether the particle should be re-initialized or not. The "steplength" for the 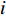th particle at the 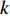th iteration (denoted by 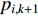) is given by:

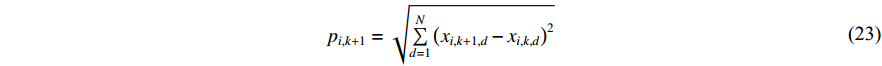
where 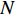 denotes the dimension of the problem space. If the 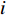th particle's "steplength" is below the threshold, the 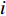th particle will be put into an "inactive particles" group. When  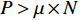(where  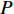denotes the size of the "inactive particles" group, and  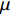is a design parameter), we need to re-initialize the particles in the "inactive particles" group. Based on a probability 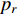, a number of particles are re-initialized with new velocities, positions and parameters, while other particles are re-initialized only with new parameters with hope to improve the convergence behavior and guarantee the solution accuracy.

In [60], two re-initialization methods have been proposed (which are the random re-initialization strategy and the elitist re-initialization strategy) to promote the PSO diversity. The first method is random re-initialization (RRPSO) where particles are reserved randomly, which could improve the ability of exploration. The second method is elitist re-initialization (ERPSO) where the worse preferred particles in the searching area are re-initialized, which could make the particle obtain a better fitness value than standard PSO.

3.2.2. Switching Strategy

So far, a new class of switching strategies have been designed for improving the PSO algorithm, where the evolution process is divided into several evolutionary states. In [61], an attractive and repulsive PSO (ARPSO) algorithm has been introduced, which is a diversity-guided optimizer that could alleviate the premature convergence. The velocity of the 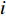th particle at the ( 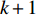)th iteration of the ARPSO algorithm is given as below:

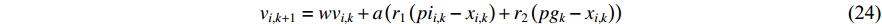
where 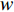 indicates the inertia weight;  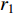and 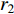 are two separate numbers randomly generated within 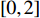;  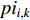represents the personal best location discovered by the 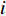th particle itself;  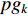represents the global best location among all candidates; and  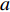is a parameter used to determine the evolution phase. The optimizer is at the repulsion phase (which demonstrates better divergence than the other evolution phase) when  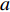is set to be 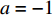. The optimizer at the attraction phase would encourage the swarm to converge when  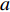is set to be .

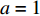In [21], an adaptive PSO (APSO) algorithm has been proposed, where an evolutionary factor (EF) is introduced to determine the exploration, exploitation, convergence, and jumping out states. The evolutionary state estimation technique and the elitist learning strategy have been proposed in the APSO. According to the ESE, the evolution process can be divided into four states based on the evolutionary factor. The EF at the 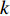th iteration (denoted by 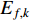) is calculated by:

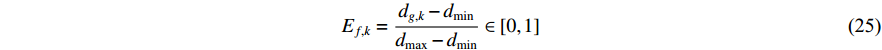
where 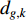 is the mean distance value of the global best particle at the 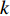th iteration to all the other particles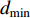; and  and 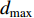 are the minimum and the maximum value of 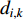, which is the mean distance value of the particle  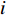to all the other particles. Note that  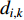is measured by using the following equation:

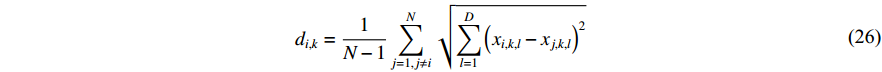
where 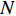 denotes the swarm size; and  is the number of dimensions. The inertia weight ( 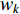) is adjusted using a sigmoid mapping based on the EF, which is shown as follows:

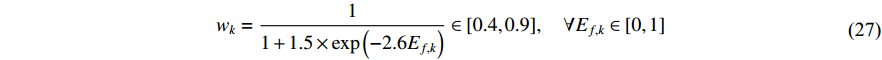
where 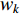 is initialized to be 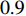, and the acceleration coefficients are initialized as  and adjusted according to the evolutionary state. The main steps of the APSO algorithm are presented in Algorithm 2. Compared with the standard PSO algorithm, the APSO algorithm demonstrates better performance in terms of the convergence speed, global optimization ability and solution accuracy.

In [18], a switching-motivated PSO algorithm (SPSO) has been developed. Based on the evolutionary factor, the velocity updating process could jump from one state to another by using a Markov chain, and the acceleration factors are thus updated based on the evolutionary state. Furthermore, a leader competitive penalized multi-learning approach is introduced in order to help the globally best particle slip away from the local optimal areas and accelerate the convergence speed. The velocity updating equation of the 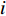th particle at the ( 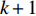)th iteration of the SPSO algorithm is expressed as follows:

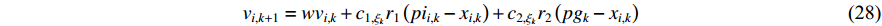
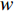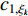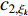where  indicates the inertia weight;  and  are acceleration coefficients;  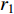and 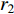 are two separate random numbers generated within 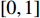;  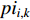represents the personal best position found by the 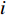th particle itself;  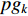represents the global best position of the entire swarm; and  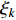is a non-homogeneous Markov chain which is used to determine the parameters. Different from the APSO, the mean distance value of the 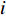th particle to all the other particles (denoted by 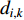) is calculated as follows:

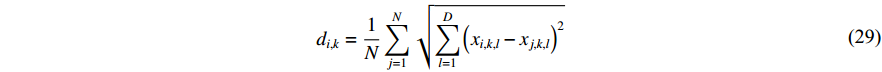
where 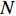 is the swarm size; and  is the number of dimensions. The EF can be calculated based on Equation (25). After calculating the EF, the evolutionary state can be confirmed based on the Markov chain. The parameters of the SPSO are mode-dependent. The inertia weight ( 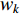) of the SPSO algorithm is expressed by:

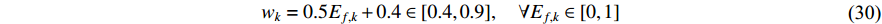
where 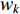 is initialized to be 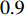; and 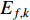 is the EF. The values of the acceleration coefficients are listed in Table 4.

Table 4. Acceleration Coefficient Updating Strategies of the SPSO Algorithm

Evolutionary State	Ef,k	ξk	c1,ξk	c2,ξk
Convergence	[0, 0.25)	1	2	2
Exploitation	[0.25, 0.5)	2	2.1	1.9
Exploration	[0.5, 0.75)	3	2.2	1.8
Jumping-out	[0.75, 1]	4	1.8	2.2

The steps of the SPSO algorithm are presented in Algorithm 3.

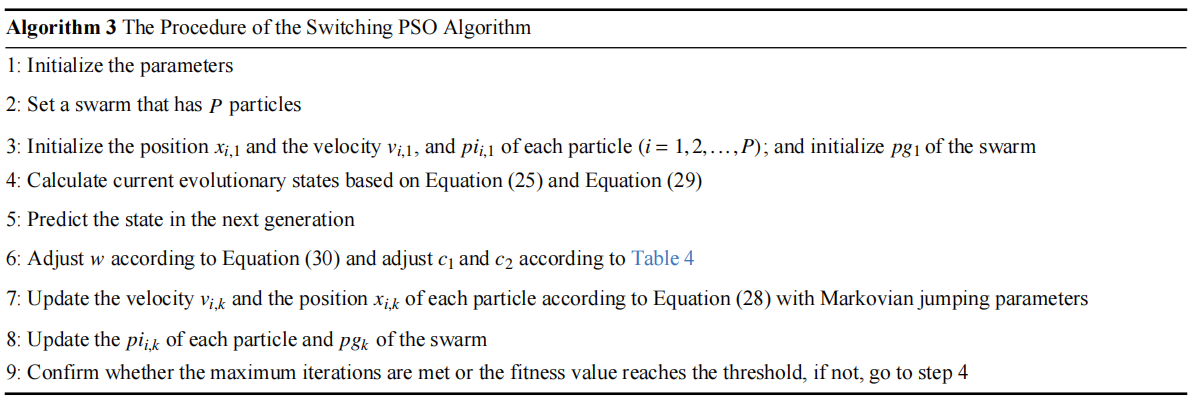
In [24], A dynamic-neighbourhood-based SPSO (DNSPSO) algorithm has been developed, where the evolution information of the swarm is used in the velocity updating process based on (1) a distance-based dynamic neighbourhood; and (2) the switching strategy. The velocity of 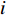th particle at the ( 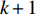)th iteration can be calculated by:

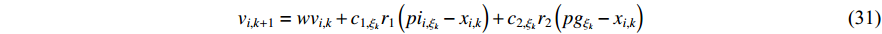
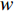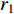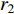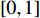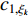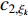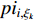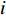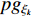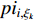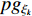where  denotes the inertia weight;  and  are two random numbers selected from ;  and  are acceleration coefficients;  represents the personal best position found by the th particle itself;  represents the global best position of the entire swarm;  denotes four different evolutionary states. Note that  and  are updated based on the dynamic neighbourhood. The evolutionary state can be calculated according to Equation (25) and Equation (26) [21]. The DNSPSO algorithm improves the solution accuracy and enhances the particle's ability of slipping away from the local optima comparing with the SPSO algorithm. The technical details of the DNSPSO algorithm are summarized in Table 5.

Table 5. Velocity Updating Strategies of the DNSPSO Algorithm

Evolutionary State	Ef,k	ξk	c1,ξk	c2,ξk
Convergence	[0, 0.25)	1	2	2
Exploitation	[0.25, 0.5)	2	2.1	1.9
Exploration	[0.5, 0.75)	3	2.2	1.8
Jumping-out	[0.75, 1]	4	1.8	2.2

Based on the SPSO algorithm, an improved SPSO (ISPSO) algorithm has been introduced in [62], where a non-stationary multistage assignment penalty function is introduced. The updating strategy of velocity jumps from each mode based on the non-homogeneous Markov chain, which uses the swarm diversity as the current search information to adjust the probability matrix in order to balance the global and local search.

In [23], a switching time-delay-embedded PSO (SDPSO) algorithm has been introduced, where the time delay is employed to alter the system dynamic of the SPSO algorithm. The utilized time delays contain the historical information of the evolutionary process. The velocity and position of the 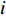th particle at the ( 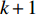)th iteration are given as follows:

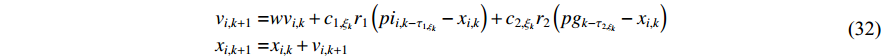
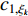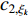where  and  are acceleration coefficients;  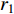and 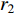 are two separate random numbers generated within 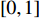;  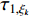and 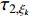 denote the delay;  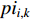represents the personal best location found by the 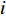th particle itself;  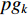represents the global best location of the entire swarm; and  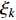is a non-homogeneous Markov chain which is used to determine the parameters. The updating strategies of the inertia weight and acceleration coefficient are same as the SPSO algorithm. The convergence speed and the global optimality of the SDPSO algorithm are competitive by comparing with some existing PSO variants.

The multi-modal delayed PSO (MDPSO) method has been developed in [63], where the so-called multi-modal time-delay is embedded into the velocity model to enlarge the search space and reduce the probability of being trapped in the local optima. In the MDPSO algorithm, the velocity updating equation of the 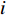th particle at the ( 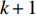)th iteration is given by:

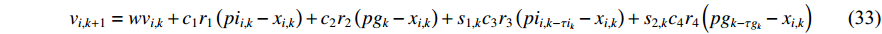
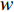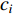
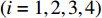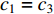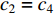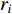
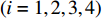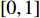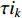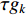where  denotes the inertia weight;   are the acceleration coefficients where  and ;   are random numbers from ;  and  indicate the randomly generated time-delays within  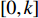of the local and global best particles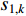; and  and 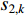 are two intensity factors. The velocity updating strategy of the MDPSO algorithm is summarized in Table 6.

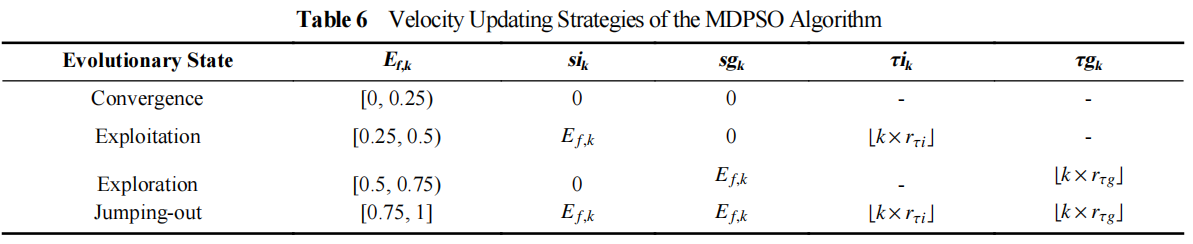
In Table 6, 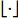 represents the round down function.  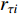and 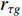 are two random numbers uniformly selected from 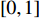. The MDPSO algorithm is able to reduce the probability of trapping into the local optima with satisfactory convergence rate.

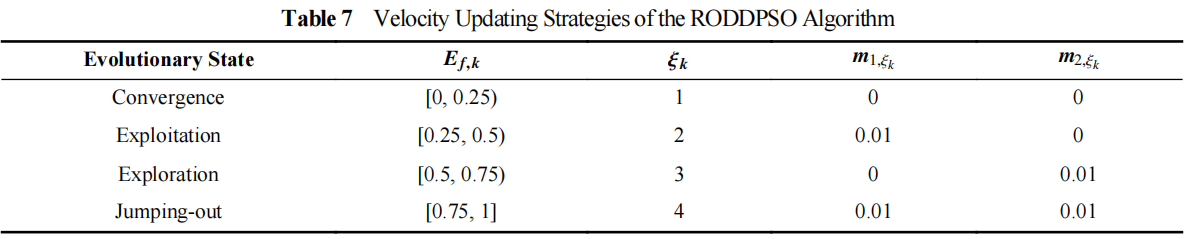
A novel randomly-occurring-distributed-time-delay PSO (RODDPSO) algorithm has been proposed in [22], where the distributed time-delays are employed to perturb the dynamic behaviour of the particles. The delays occur randomly, which contributes to a better search ability than the SDPSO. The velocity of the 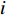th particle at the ( 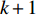)th iteration is updated by:

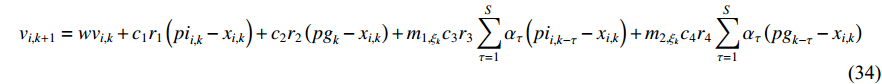
where 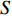 denotes the upper bound of the distributed time-delays;  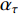is a vector with 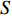-dimension, and each member of  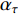is chosen from 0 or 1 randomly;  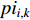represents the personal best position found by the 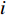th particle itself;  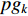represents the global best position of the entire swarm;  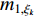and 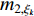 indicate the intensity of the distributed time-delays; and  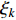denotes the current evolutionary state. The evolutionary state is determined by Equation (25) and Equation (26) [21]. The velocity updating strategy of the RODDPSO algorithm at each evolutionary state is summarized in Table 7.

In [64], a modified switching PSO algorithm with adaptive random fluctuations (ARFPSO) has been introduced, where the velocity is updated based on the evolutionary states, and the adaptive random fluctuations are added to the pbest and the gbest particles. According to the simulation results reported in [64], the ARFPSO algorithm shows superior performance in terms of search the optimal solution.

In [65], a PSO algorithm with fractional velocity (FVPSO) has been developed, where the fractional-order velocity terms are added to the velocity updating equation. The FVPSO algorithm enhances the particle's ability of jumping out of the local optima. Based on the FVPSO algorithm, an adaptive fractional-order velocity SPSO (FVSPSO) algorithm has been presented in [66], where the fractional velocity is updated based on the evolutionary state. The velocity of the 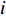th particle at the ( 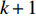)th iteration of the FVSPSO algorithm is updated by:

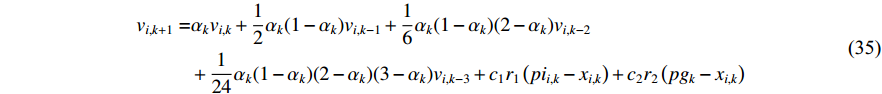
where 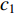 and 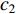 are acceleration factors; 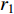,  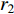are two random numbers in 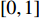;  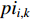is the personal best position found by the 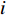th particle itself;  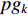represents the global best position of the entire swarm; and  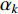denotes the fractional order of the velocity, which can be calculated by:

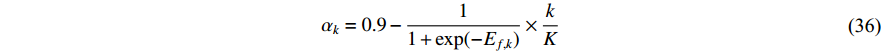
where 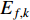 represents the evolutionary factor obtained by Equation (25) and Equation (26) [21]. The FVSPSO algorithm improves the search ability and could make the particles easily jump out of the local optima.

The asynchronous PSO algorithm has been brought up in [67]. Compared with the standard PSO method, the asynchronous PSO method exhibits faster convergence rate. The asynchronous updating strategy could delay the convergence of the swarm, while the synchronous updating strategy could accelerate the convergence [68]. In [58], an adaptive switching asynchronous-synchronous PSO (SASPSO) algorithm has been proposed, where the asynchronous updating strategy and the synchronous updating strategy are hybridized, which could switch from one to another according to the fitness value of the gbest.

In [69], the clustering algorithm has been utilized in the PSO (CAPSO) algorithm to group the particles based on their previous best positions, and the cluster centroids are replaced by particles' personal best positions and neighbours best positions. According to the experimental results reported in [69], it is found that the CAPSO algorithm (using personal best positions as the cluster centroids) performs better than algorithms using neighbours’ best positions as cluster centroids.

The constriction factor and its variants have been put forward in [46, 70, 71], which improves the convergence rate of the optimizer by limiting the motion of individuals in the optimal region. The velocity and position of the PSO algorithm with constriction factors (CFPSO) are updated by:

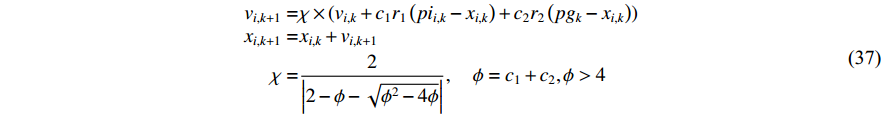
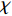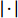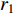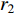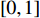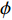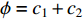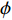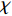where  is the constriction factor;  is the absolute value of " ";  and  are two constants randomly generated within ; and  is a parameter to adjust the constriction factor where . Normally,  and  are set to be  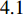and 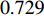, respectively.

In [72], two cooperative PSO (CPSO) algorithms have been proposed (i.e., CPSO- 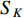 and CPSO- 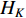), where the cooperative behaviours are utilized to improve the solution accuracy.

In [34], a comprehensive learning (CL) strategy has been proposed, where the particle's velocity is updated according to the personal best locations of all other particles. The CLPSO algorithm demonstrates better performance in solving muti-modal problems compared with the standard PSO algorithm. The velocity of the 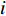th particle at the ( 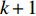)th iteration of the CLPSO algorithm is shown as follows:

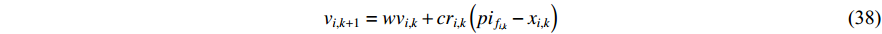
where 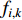 represents which particle's pbest should be followed by the 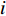th particle. The learning probability  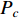decides which particle should be chosen for the 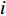th particle to learn from. More specifically, a number of random numbers are created based on the dimensions of the 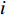th particle. If the random number is larger than 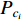, the particles will learn from its own pbest at the corresponding dimension. Otherwise, the particle will learn from another one's pbest by using a tournament selection procedure at the corresponding dimension.

In [73], a multi-elitist PSO algorithm (MEPSO) has been introduced, where the multi-elitist strategy has been employed in the PSO algorithm to improve the global search, which improves the search ability of the PSO algorithm.

In [27], a field-programmable gate array (FPGA)-based parallel meta-heuristic PSO (PMPSO) algorithm has been proposed, which employs the parallel computing strategy to run three parallel PSO algorithms in the same FPGA chip. According to the experimental results reported in [27], the PMPSO algorithm shows the merit in solving some global path planning problems.

An improved PSO algorithm with a detection function (IDPSO) has been presented in [74], where the control parameters are updated based on the detection function. The control parameters (i.e., 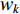,  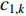and 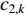) at the 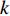th iteration are updated by:

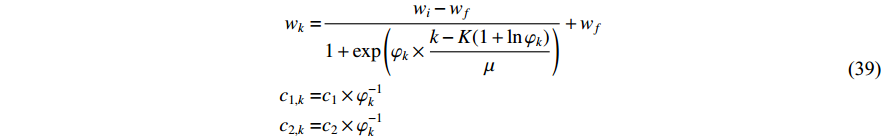
where 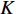 is the maximum iteration number;  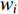and  represent the initial and final inertia weight, respectively;  represents the detection function; and  is an adjustment factor. The IDPSO algorithm improves the search ability of the particle.

In [75], the quantum PSO (QPSO) algorithm has been proposed, where the quantum theory is introduced into the PSO algorithm. A trial method for adjusting parameters has also been proposed. A new parameter tuning method has been put forward in [76] to adjust the control parameters of the QPSO algorithm, where a global reference point has been introduced to evaluate the search range of the particle. The QPSO algorithm with the new parameter selection strategy has shown better performance than the standard QPSO algorithm in terms of convergence and solution accuracy.

3.3. Improving Topological Structures

Developing new topological structures becomes a popular way to design PSO algorithms. A lot of topological structures have been put forward to improve the performance of the PSO algorithm. The reviewed approaches on developing new topological structures of the PSO algorithm are summarized in Table 8.

Table 8. Improving Topological Strategies of the Algorithm

Approach	Abbreviated Name	Reference
Neighborhood Operator	NOPSO	[16]
Fitness-distance-ratio Based	FDR-PSO	[81]
Dynamic Multi-swarm	DMSPSO	[82]
Hierarchical Structure	HPSO	[11]
	AHPSO	[11]
Niching	NPSO-1	[85]
	SBPSO	[86]
	ANPSO	[84]
	DLIPSO	[87]
	TPSO	[83]

The neighbour of each particle can be divided into two categories (including the local best (i.e., lbest) and the global gbest (i.e., gbest)), which is depicted in Figure 3 [77]. The particle in the lbest neighbourhood is affected by its immediate neighbours’ best performance. The particle in the gbest neighbourhood is attracted to the best solution found by the entire swarm.

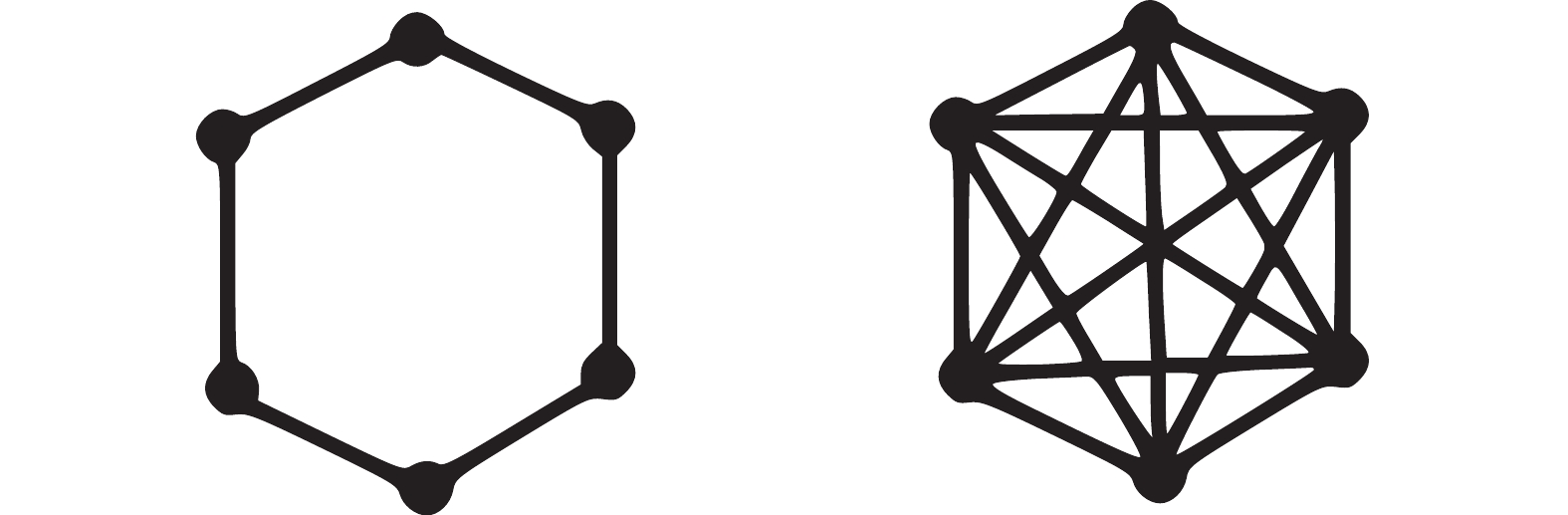
Figure 3. The lbest (left) and the gbest (right) topologies of the PSO algorithm.

The social network topology of the swarm has been modified in [78], which shows that the impact of the topology is different based on the objective function. PSO algorithms using different topological structures (including the lbest, the gbest, the pyramid, the star, the "small", and the von Neumann) have been evaluated and discussed in [79]. The experimental results reported in [79] indicate that the von Neumann configuration has consistent performance. In [80], a fully informed PSO algorithm has been put forward, where the velocity of the particle is updated according to the information from its neighbours. The network topologies of the star and the von Neumann are shown in Figure 4.

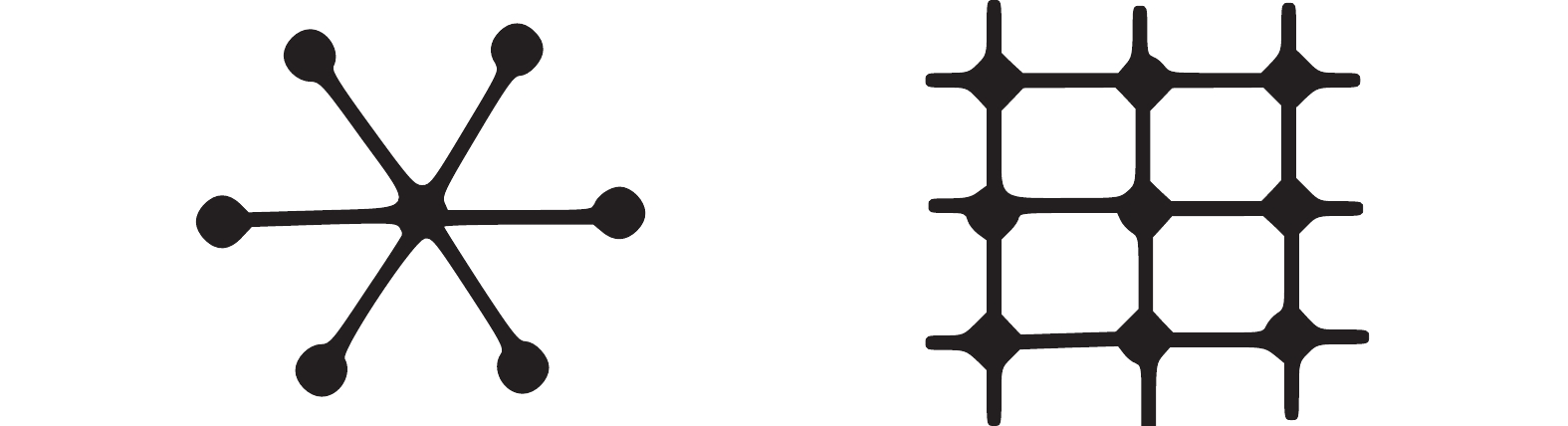
Figure 4. The star (left) and the von Neumann (right) topologies of the PSO algorithm.

In [16], the PSO algorithm with the variable neighbourhood operator (NOPSO) has been introduced, where the size of the lbest neighbourhood increases gradually until the whole swarm is connected during the evolutionary process. It should be noted that the gbest is replaced by the lbest solution to improve the search ability and avoid the local optima, which means the information is only shared locally. The neighbours can be defined by either the position compared with other particles or the proximity [32].

In [81], a fitness-distance-ratio based PSO (FDR-PSO) algorithm has been proposed, where the FDR is used to calculate the nbest. Note that nbest represents a particle's best nearest neighbour, which is used to update the particle's velocity. The velocity of the 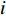th particle at the ( )th iteration is updated by:

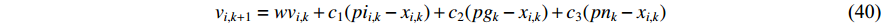
where 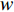 is the inertia weight; 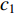,  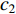and 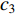 are the acceleration coefficients;  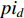represents the personal best position found by the 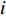th particle itself;  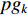represents the global best position of the entire swarm; and  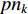represents the historical best experience of the nbest. The velocity is updated according to three factors, which are the pbest, the gbest and the historical best experience of the nbest. The FDR-PSO algorithm could alleviate the premature convergence during the evolutionary process.

In [82], a dynamic multi-swarm PSO (DMSPSO) algorithm has been introduced, where the swarm is divided into many small swarms and randomized frequently. Each small swarm searches the solution by itself in the search space. In order to improve the information exchange, a randomized regrouping schedule is introduced, where the population is regrouped randomly at every iteration and begins to search with a new configuration of small swarms. This neighbourhood structure shows competitiveness in solving complex multi-modal problems.

In [11], a hierarchical PSO (HPSO) algorithm has been proposed, where the particles are placed in a dynamic hierarchy and moved in the hierarchy according to the discovered best solution. The HPSO variants have been developed by adjusting the inertia weight. The updating rules of the inertia weights ( 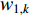 and 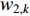) are given below:

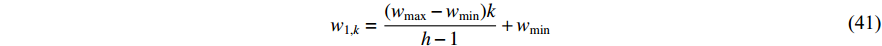
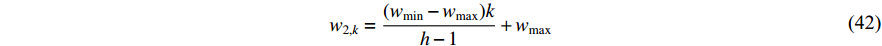
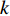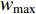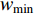where  denotes the level of the hierarchy;  and  are the maximum and minimum of the inertia weight, respectively; and  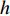is the maximum level of the hierarchy. The 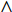HPSO algorithm uses Equation (41) to update the inertia weight (i.e., 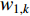), where the inertia weight of the root particle is denoted by 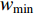. The inertia weight of the 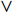HPSO algorithm (i.e., 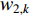) is updated by Equation (42), in which  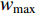represents the inertia weight of the root particle. According to the experimental results reported in [11], the HPSO algorithm shows satisfactory performance for both uni-modal and multi-modal optimization problems.

Inspired by the GA, niching is employed in PSO so as to increase the number of solutions for multi-modal optimization problems. Niching divides the swarm into several parts to explore the optimal region as much as possible. Recently, a few niching PSO methods have been developed [83-87]. In [85], a niching PSO (NPSO-1) algorithm has been proposed to solve the multi-modal problems. Each particle searches in the problem space separately until the variance of the particle's fitness values of the last three iterations is smaller than a threshold. Then, a sub-swarm of this particle and its nearest topological neighbour is generated. It is worth mentioning that other particles can join the sub-swarm when they move into the area of the sub-swarm. The NPSO-1 algorithm improves the search ability and the convergence accuracy.

In [86], a species-based PSO (SBPSO) algorithm has been developed, where all individuals are divided into a number of sub-groups of individuals based on the similarity. Different species would not share information with each other, which enhances the search performance of the algorithm when solving multi-modal optimization problems. In [84], a niching PSO algorithm with an adaptively niching parameters choosing strategy (ANPSO) has been proposed, where the statistical information of the population is utilized to adaptively update the niching parameters so as to improve the convergence rate and the solution quality of the optimizer. In [87], a distance-based locally informed PSO (DLIPSO) algorithm has been developed, where a number of lbests are utilized to guide each particle's search, which improves the search ability and avoids specifying the niching parameters.

3.4. Hybridizing with the EC Algorithms

Hybridizing with other optimization algorithms is also an important method for improving PSO algorithms. Many EC algorithms have been combined with the PSO algorithm so as to further improve the searching performance of the optimizer. The reviewed approaches on hybridizing with other EC algorithms are summarized in Table 9.

Table 9. Hybridizing the PSO Algorithm with Other EC Algorithms

Approach	Reference
Hybridizing with the GA	[25, 88, 89, 92, 93, 95-97, 98-100]
Hybridizing with the ACO Algorithm	[101]
Hybridizing the SA Algorithm	[12]
Combining with the Nelder-Mead Algorithm	[102]
Combining with the Differential Evolution	[26]

3.4.1. Hybridizing with the GA

The genetic algorithm is inspired by biological evolution, which contains lots of computational models. So far, some researchers have focused on combining the GA and the PSO algorithm to further improve the performance (e.g. convergence performance and global search ability) of the PSO algorithm.

In [88], three hybrid algorithms have been proposed, where the modification strategies using the GA are employed in the PSO algorithm. In the first strategy, the position of the gbest particle is not changed at some assigned iterations, and the crossover operation is applied to perturb the gbest. In the second strategy, the positions of pbest particles which are slow or stagnated are changed by a mutation operator. In the third strategy, the searching process is equally divided into two parts, where the first part runs the GA and the second part runs the PSO algorithm. In the PSO part, the initial swarm is assigned by using the solution of the GA. According to the experimental results reported in [88], three algorithms exhibit satisfactory convergence rate.

A PSO algorithm with the EC-based selection mechanism has been introduced in [89], where a form of tournament selection is also developed. By comparison of the particles' current fitness, the particles can be divided into two parts. The selection mechanism could change the values of the current positions and velocities of the "bad" half of the population by using the values of the "good" half of the population without changing the pbest of particles.

It is known that the mutation is an important step in the GA. Recently, the mutation operator has become an important method in developing EC algorithms, which could (1) prevent the loss of the population diversity to some extent; and (2) expand the search space [90]. The mutation operator could add new individuals to the population by creating a variation so that the population diversity can be improved [91].

In [92], a PSO algorithm with the Gaussian mutation operator has been proposed, where the dimension of the particle's position is changed by the mutation operator which obeys the Gaussian distribution. The Gaussian mutation operator (denoted by 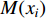) is shown as follows:

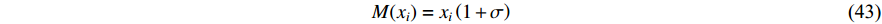
where 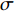 is a random number which obeys the Gaussian distribution.

A mutation operator has been added to the PSO algorithm in [25], where a random number drawn from a Cauchy distribution is added to the component that needs to be mutated. The improved PSO algorithm with the proposed mutation operator improves the convergence rate of the optimizer and the ability of escaping from the local optima. The mutation operator (denoted by 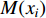) is expressed as follows:

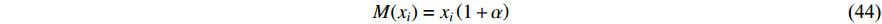
where 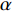 is a random number which obeys the Cauchy distribution. The components of the particle (chosen to be mutated) is randomly selected with the probability 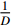.  is the dimension of the particle.

In [93], a PSO algorithm with a nonuniform mutation operator (designed in [94]) has been developed. The operator works by changing the dimension of each individual particle. By using the nonuniform mutation operator, the performance of the PSO algorithm is improved especially for handling multi-modal problems.

In [95], a learning strategy and a mutation operator named Gaussian hyper-mutation have been added to the asynchronous PSO algorithm in order to enhance the convergence and maintain the population diversity.

The linkage is a concept in the GA algorithm. In [96], a linkage-sensitive PSO (LSPSO) algorithm has been introduced, where the elements of a linkage matrix are employed. The linkage matrix is calculated based on the performance of some randomly generated particles with perturbations. The positions of the particles which are linked are updated at the same time.

In [97], a PSO algorithm with recombination and dynamic linkage discovery (PSO-RDL) has been presented. A dynamic linkage discovery strategy is designed, where a linkage configuration is updated according to the fitness value, which is easy to implement and has a high efficiency. During the evolutionary process, a number of linkage groups are assigned, and the linkage configuration is adjusted according to the fitness value. If the average fitness value meets the threshold, the current linkage configuration will not be changed. Otherwise, the linkage groups will be reassigned randomly. In addition, a recombination operator has been designed to generate the next population by choosing and recombining building blocks from the pool randomly. The PSO-RDL algorithm shows competitive performance compared with several selected PSO variants.

In [98], a hybrid PSO algorithm with breeding and sub-populations has been developed. The population is divided into several sub-populations. Two particles are chosen randomly for breeding, and the arithmetic crossover is used during the breeding process. The parents are replaced by the offspring at the end of each iteration. The positions of the two particles (offspring) at the ( 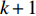)th iteration are expressed as follows:

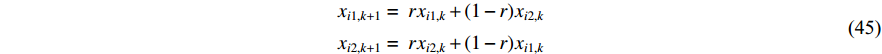
where 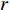 is the random number in 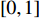. The hybrid PSO algorithm with breeding and sub-populations obtains faster convergence rate than that of the standard PSO algorithm as well as the standard GA.

A PSO algorithm with the novel multi-parent crossover operator and a self-adaptive Cauchy mutation operator (MC-SCM-PSO) have been developed in [99], where the particle influenced by the multi-parent crossover operator can learn from three particles in the neighbourhood. The position of the offspring at the ( 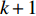)th iteration of the introduced algorithm is calculated as:

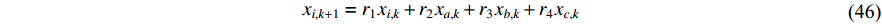
where 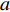, , 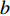and 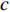 are three selected particles; and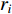 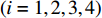  are four random numbers selected from . The MC-SCM-PSO algorithm could greatly increase the chance of slipping away from the local optima especially when solving multi-modal optimization problems.

In [100], six PSO variants with discrete crossover operators have been proposed, which choose the second parents and the number of crossover points in different ways. Experimental results show that two proposed PSO variants outperform the standard PSO algorithm.

3.4.2. Hybridizing with Other Evolutionary Methods

Apart from the GA, the PSO algorithms have also been hybridized with some other EC methods (such as the ACO algorithm, the SA algorithm and the differential evolution (DE) algorithm) with the purpose of improving its performance in convergence and solution accuracy.

In [101], a hybrid optimization algorithm which combines the FAPSO algorithm with the ACO algorithm (FAPSO-ACO) has been presented, where the control parameters of the FAPSO algorithm are adjusted according to the fuzzy rules. The decision-making structure is added to the FAPSO algorithm, which improves the performance of the PSO algorithm. In [102], the FAPSO algorithm has been combined with the Nelder-Mead (NM) simplex search, where the NM algorithm is considered as a local search algorithm to search around the global solution, which significantly improves the performance of the FAPSO algorithm.

The hybridization of PSO and SA (PSO-SA) has been introduced in [12]. The SA algorithm is utilized to search the global solution, and a mutation operator is used to enhance the communication between particles. According to the experimental results reported in [12], the PSO-SA algorithm has fast convergence rate and high accuracy.

Based on [18] and [62], the switching-local-evolutionary-based PSO (SLEPSO) algorithm has been developed in [26]. In SLEPSO, ISPSO is integrated with DE, and thus improves (1) the search ability of the current local best particles; and (2) the chance of slipping away from the local optima.

4. Applications of the PSO Algorithm

In this section, some selected practical applications of the PSO algorithm are reviewed, which are divided into 6 categories including robotics, the renewable energy system, the power system, data analytics, image processing and some other applications.

4.1. Robotics

4.1.1. Path Planning for Robots

Autonomous navigation of the mobile robot is a crucial task in robotics. The autonomous navigation process is illustrated in Figure 5. As an important task in autonomous navigation, path planning has been widely investigated, which is known as an optimization problem in certain indices with some certain constraints [103-105]. So far, a number of PSO algorithms have been adopted to solve the robots path planning problems.

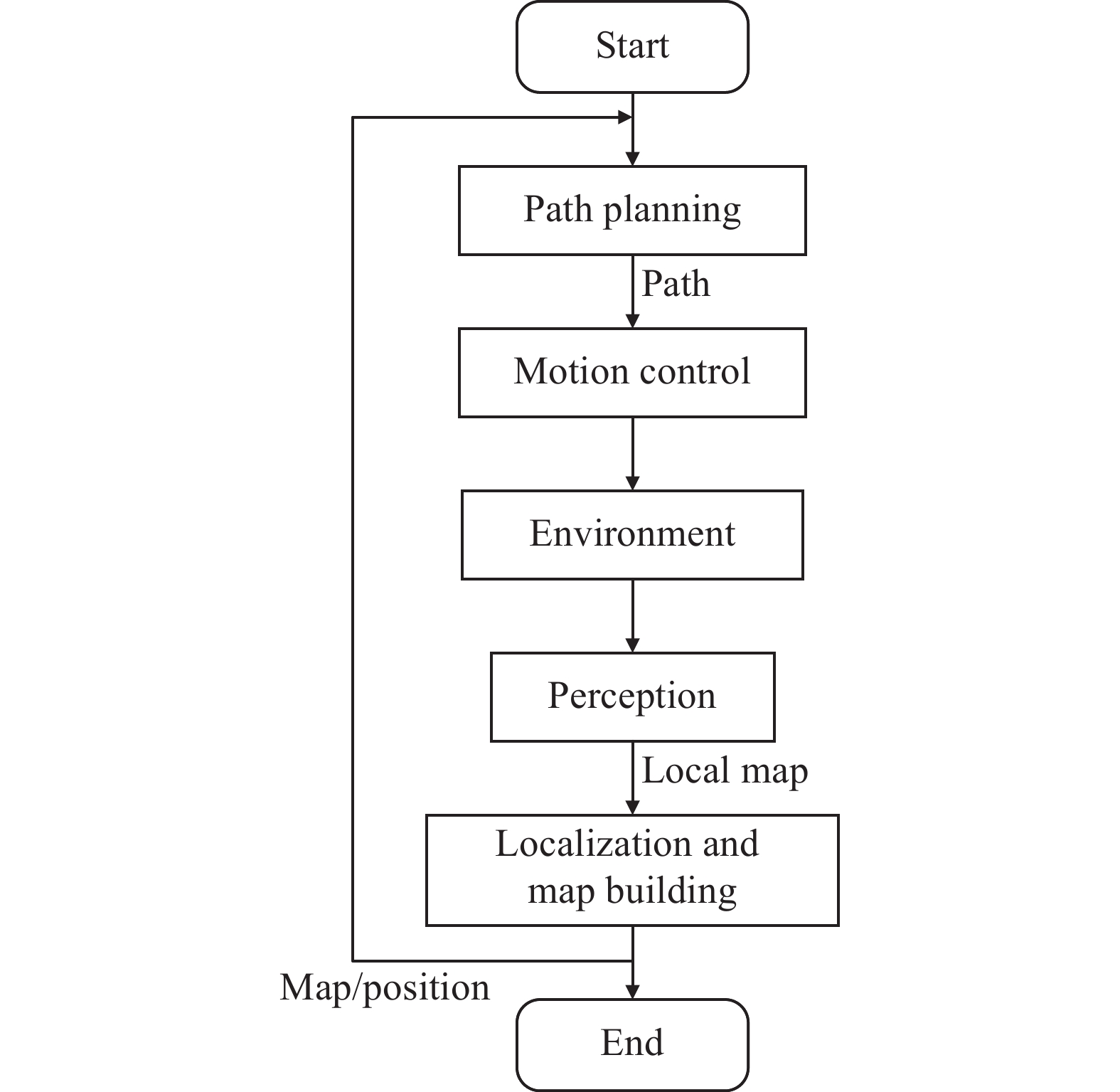
Figure 5. The autonomous navigation process of the mobile robot.

In [27], the PMPSO algorithm has been applied to deal with the navigation of the autonomous robot in structured environments with obstacles. In [106], the SLEPSO algorithm has been used to solve the path planning problem of the intelligent robot. In [63], the MDPSO algorithm has been successfully applied to the path planning for mobile robots. In [107], the novel Chaotic PSO method has been put forward to tackle the path planning problem by optimizing the control points of Bezier curve. In [64], a switching PSO algorithm with adaptive random fluctuations has been combined with the 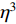-splines to solve a double-layer smooth global path planning problem with several kinematic constraints. In [66], the FVSPSO algorithm has been applied for smooth path planning for the mobile robots based on the continuous high-degree Bezier curve.

4.1.2. Robot Learning

The purpose of robot learning is to teach robots to learn skills and adapt to the environment under the guidance of learning algorithms. As an efficient class of EC algorithms, the PSO-based robot learning algorithms have been employed in the robot learning field. In [108], a PSO-based robotic learning method has been proposed, where a noise reduction technique used in the GA has been applied to the PSO algorithm to improve the performance of robot learning. In [109], an adapted PSO algorithm has been applied for unsupervised robotic learning, which shows competitiveness over some existing ones. In [110], an improved PSO-based method has been utilized in robot learning, where a statistical technique, named the optimal computing budget allocation, is utilized to improve the performance of the PSO algorithm with noises.

4.2. Renewable Energy System

In recent years, the utilization of the alternative energy has increased significantly in order to fulfil the requirements of environmental protection and electricity demands. Figure 6 shows a structure of the basic alternative energy system. In this case, the optimal designing plans of the energy system has been made to utilize the energy resources efficiently and economically. In recent years, a number of PSO-based approaches have been put forward for solving the optimization problems in energy systems [111, 112].

Figure 6. A basic alternative energy system with battery storage.

4.2.1. Sizing

The sizing problem is an important optimization problem in energy systems, which aims to find the optimum number and types of devices to be used [112]. The optimum unit size can ensure the system working in the best conditions with the lowest cost, which could keep the system efficient and economic [111]. In recent years, many PSO-based methods have been developed to solve the sizing problem in energy systems.

In [113], the GA and the PSO algorithm have been used to optimize the unit size of the stand-alone hybrid energy system. A PSO-based approach has been proposed in [114] to solve the sizing problem of a hybrid solar photovoltaic energy system. In [115], the PSO algorithm has been applied to a new hybrid renewable energy system. In [116], the PSO algorithm has been applied to the sizing problem of the distributed energy system in micro grid.

4.2.2. Maximum Power Point Tracking

The maximum power point tracking (MPPT) on the solar photovoltaic module of the energy system is also a challenging optimization task, which aims to help the solar photovoltaic module produce maximum power output [112]. In recent years, a number of MPPT approaches have been developed. Among the proposed approaches, the PSO-based methods have demonstrated better noise immunity, which has become a popular way to track the maximum power point [8].

In [8], a tracking method has been proposed where the PSO algorithm has been used to recognize the maximum power point in the photovoltaic system with high efficiency and fast convergence rate. In [28], a PSO-based MPPT controller of the photovoltaic system has been introduced by using the direct control method. In [117], a MPPT method with an improved PSO algorithm has been presented where the steady-state oscillations are decreased when the maximum power point is found, which could reduce the tracking time. In [118], a 3-phase 4-wire current-controlled voltage source inverter with the PSO-based maximum power point tracking method has been developed where the PSO-based maximum power point tracking method searches independently while the control loops are working. The developed PSO-based maximum power point tracking method could improve the power quality and enhance the photovoltaic energy extraction ability. In [119], an improved PSO algorithm with the catastrophe theory has been introduced for maximum power point tracking [120]. In [121], a new maximum power point tracking approach with the PSO algorithm has been proposed, where the multiple photovoltaic arrays are controlled by only one pair of sensors. Results show that the developed method reduces the cost and improves the efficiency of the system. In [122], an MPPT algorithm has been put forward for detecting the global maximum power, where the PSO algorithm is embedded into the artificial neural network.

4.2.3. Others

In [123], a PSO algorithm with the constriction factor and the mutation operator has been applied to solve the capacity configuration problem. The PSO algorithm has been used in [124] to identify the parameters of the photovoltaic model. In [125], a parameter optimizing method of the current control strategy for a 3-phase photovoltaic grid-connected voltage source inverter system has been proposed, where the PSO algorithm is used to tuning the current control parameters. Results show that the optimized system improves the power quality.

4.3. Power System

4.3.1. Economic Dispatch

Economic dispatch (ED) problem has become a popular research topic in the power system, which plays a crucial role in the operation and planning of the power system. The ED problem aims to adjust the output of generating units in order to meet the load requirement with the lowest cost and also satisfy the operational constraints of units as well as the system [126]. In fact, the ED problem can be treated as the optimization problem, and a large number of optimization techniques have been adopted to solve the ED problem.

In [97], the PSO-RDL algorithm has been applied to the economic dispatch problem for the 3-unit power system and has discovered the currently best solution for the 40-unit system. In [127], the combined economic and emission dispatch (CEED) problems have been handled by using the PSO algorithm. In [30], an improved PSO algorithm with the constriction factor has been put forward to deal with the bid based dynamic ED problem. The PSO algorithm has been hybridized with the sequential quadratic programming (SQP) method to deal with the ED problem with the valve-point effects [128]. In [129], a CEED problem (which considers the fuel cost, the emission and the variance of generation mismatch) has been figured out by using the PSO algorithm. In [130], the PSO algorithm has been combined with the Gaussian probability distribution functions to solve the economic cost dispatch problem. In [131], an improved PSO algorithm has been employed to the economic load dispatch problem, where the inertia weight of the PSO algorithm is adaptively adjusted according to each particle's rank. The presented FAPSO-NM algorithm has been employed in [102] to figure out the economic dispatch problems of two systems consisting of  and  thermal units with satisfactory performance.

4.3.2. Others

The unit commitment (UC) is an efficient way to provide high-quality electric power to customers securely and economically [132]. The UC problem aims to find the optimal UC, which is an optimization problem. In [133], the FAPSO-based method has been developed to compute the UC of the power system.

4.4. Data Analytics

4.4.1. Clustering

Clustering algorithms organize a collection of similar items into the same cluster. An illustration of clustering is in Figure 7, where each point represents an instance in the data set. It is known that clustering plays a vital role in data analysis. Unfortunately, some studies have shown that the clustering performance of the distance-based clustering algorithms is highly dependent on the initial value of the clustering centroids and may be unsatisfactory when dealing with some complex data sets [73, 134]. In the past few years, some researchers have employed optimization algorithms to choose optimized location of the initial cluster centroids to improve the performance of distance-based clustering algorithms.

Figure 7. An illustration of a cluster analysis output.

In [31], a new K-means-based clustering method has been proposed, where the basic K-means clustering approach is combined with the Nelder-Mead simplex search approach and the standard PSO approach. In [101], the FAPSO-ACO algorithm has been embedded in improving the basic K-means approach. The RODDPSO algorithm presented in [22] has been utilized for improving the performance of the basic K-means approach. In [12], the PSO-SA algorithm has been embedded into K-means. In addition, PSO has also been utilized for optimizing the fuzzy c-means (FCM) algorithm [135, 136]. In [137], a hybrid fuzzy clustering algorithm has been proposed, where the FCM algorithm and a fuzzy PSO algorithm are combined. In [138], two improved FCM algorithms based on the IDPSO algorithm proposed in [74] have been developed, both of which demonstrate fast speed and high solution quality. A novel clustering algorithm has been introduced in [139], where the FCM algorithm is combined with the QPSO algorithm. The performance of the new method outperforms some other clustering algorithms [75].

Apart from the K-means algorithm and the FCM algorithm, some other PSO-based clustering algorithms have also been developed [140]. For example, in [141], PSO has been applied to the self-organizing maps (SOM), where a conscience factor is added to the SOM. The weights of the SOM are tuned by PSO, which could improve the robustness of the clustering algorithm. The MEPSO-based automatic kernel clustering algorithm has been introduced in [73], where the MEPSO algorithm is used to find the optimal number of clusters, and a kernel function is applied to cluster data in a high-dimensional transformed space.

4.4.2. Feature Selection

As an important member in data mining, classification aims to classify data into different categories based on the features of data. Nevertheless, selecting useful features in the data set is a difficult task. Some PSO-based approaches have been introduced with the purpose of dealing with the feature selection problems. A self-adaptive PSO algorithm has been introduced and applied in feature selection [142]. In [143], two PSO-based multi-objective feature selection methods have been proposed, where the non-dominated sorting idea is employed in the first method, and the crowding, mutation as well as dominance are applied to the second method. Both methods could automatically discover a set of non-dominated solutions.

4.5. Image Processing

Image processing is an important field in computer science, which includes image segmentation, image enhancement and so on. In recent years, a number of PSO-based algorithms have been proposed to improve the performance of image processing [9, 144-147].

4.5.1. Image Segmentation

Image segmentation focuses on analysing and interpreting the images. Many image segmentation methods have been developed by using PSO algorithms for improving the performance of image segmentation [144, 145, 147].

In [145], a multi-level thresholding method has been proposed for image segmentation, where a fractional-order Darwinian PSO algorithm is proposed to improve the accuracy of image segmentation. In [144], PSO has been combined with the hidden Markov random field model to improve the quality of the image segmentation. A PSO-based image segmentation method has been introduced in [147], where PSO is embedded into a region-based image segmentation (also named seeded region growing) method for oriented segmentation.

4.5.2. Image Enhancement

Image enhancement is another important task in image processing. The basic PSO approach has been widely adopted for image enhancement. A PSO-based automatic image enhancement technique has been proposed in [9], where PSO has been utilized to maximize an objective fitness criterion with the purpose of enhancing the contrast and details in the picture. Results show that the PSO-based automatic image enhancement technique obtains satisfactory performance in maximizing the number of pixels in the edges. A PSO-based image enhancement method has been introduced in [146], where a parameterized transformation function and an objective criterion have been utilized to improve the performance of the image enhancement.

4.6. Others

A large number of PSO-based methods have been developed for various real-world problems [148-150]. For example, the PSO algorithm has been used in [151] for parameter identification of the permanent magnet synchronous motors. In [152], the PSO algorithm has been applied in the control theory to find the optimal parameters of the proportional-integral-derivative controller in an automatic voltage regulator system, which provides fast parameter adjusting ability and is easy to implement. In [153], a FAPSO algorithm-based optimal bidding strategy of a thermal generator in the uniform price spot market has been developed to find the optimal bidding strategy in the power market, where the operating cost function and the minimum up/down constraints are considered.

PSO has been successfully employed to solve the electromagnetics-related optimization problems. In [154], an intelligence PSO algorithm has been utilized for optimizing the electromagnetic device, where the complexity of the particle is enlarged at the group level to improve the efficiency of the optimization process.

It should be pointed out that using the PSO algorithm to design the trajectory of the spacecraft has been a popular research topic. In [155], PSO has been used to handle several space trajectory optimization tasks. In [29], a PSO-based method has been proposed to find the optimal re-entry trajectories for the spacecraft. In [156], PSO has been employed to generate the end-to-end trajectory of the hypersonic re-entry vehicle. In [157], a recovery trajectory planning method has been introduced for the recovery process of the reusable launch vehicle, which combines the PSO algorithm with the polynomial guidance law.

5. Future Research Topics

Motivated by the PSO algorithms and their applications, some possible future research topics are summarized and provided:

(1) Designing new PSO algorithms for multi-objective and many-objective optimization problems. Up to now, a number of PSO algorithms have been proposed for solving multi-objective problems such as the MC-SCM-PSO algorithm and the SBPSO algorithm [86, 99]. Nevertheless, there is still room to improve the performance of the approaches. Some novel PSO algorithms of excellent performance could be extended to solve the multi-objective problems.

(2) Embedding the quantum theory into the PSO algorithm for solving continuous optimization problems. Owing to the increasing attention on the quantum theory, the quantum-based PSO algorithm has shown great research potential on enhancing the exploration capabilities. In this case, the development of the quantum-based PSO algorithm is an attractive research topic.

(3) Applying the PSO algorithms to deep learning. The study of deep learning has become a hot research direction thanks to its powerful abilities in data analytics and artificial intelligence during the past few years. The optimization of the parameters and hyper-parameters plays a critical role in affecting the performance of the deep learning systems. In this case, the deployment of PSO algorithms in deep learning systems could be a good choice.

(4) Developing new strategies and hybridizing PSO with recently proposed EC algorithms to further overcome the challenging problem of premature convergence. When introducing certain terms (e.g., time-delays and chaos) into the PSO algorithm, the investigation of the particle trajectory and the system dynamic is another research topic.

6. Conclusion

In this paper, the details of the PSO algorithms (including the original PSO algorithm and the standard PSO algorithm) have been introduced, and a comprehensive overview of some selected PSO variants has been provided. In particular, the survey of the chosen PSO variants has been presented according to four categories, namely the PSO variants with modified control parameters, the PSO variants with new updating strategies, the PSO variants with topological structures and the PSO variants hybridized with other EC algorithms. A number of real-world applications of the PSO algorithms have been reviewed and summarized. Finally, some possible research topics have been listed for future work.

Author Contributions: Jinghzong Fang: conceptualization, methodology, writing—original draft preparation
and visualization; Weibo Liu: conceptualization, methodology, writing—original draft preparation, writing—
review and editing, supervision; Xiaohui Liu: conceptualization and methodology; Linwei Chen: methodology,
writing—review and editing and visualization;Stanislao Lauria: validation, writing—original draft preparation
and writing—review and editing;Alina Miron:validation, writing—review and editing, visualization. All authors
have read and agreed to the published version of the manuscript.

Funding: This research received no external funding.

Conflicts of Interest: The authors declare no conflict of interest.