Downloads

doi: https://doi.org/10.53941/ijndi0101010
Zhang, Q., & Zhou, Y. Recent Advances in Non-Gaussian Stochastic Systems Control Theory and Its Applications. International Journal of Network Dynamics and Intelligence. 2022, 1(1), 111–119. doi: https://doi.org/10.53941/ijndi0101010
Volume 1, Issue 1, Dec 2022
Copyright (c) 2022 by the authors.
Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Survey/review study

Recent Advances in Non-Gaussian Stochastic Systems Control Theory and Its Applications

Qichun Zhang 1, and Yuyang Zhou 2,*

1 Department of Computer Science, University of Bradford, Bradford BD7 1DP, United Kingdom

2 School of Computing, Engineering and the Built Environment, Edinburgh Napier University, Edinburgh EH10 5DT, United Kingdom

* Correspondence: y.zhou@napier.ac.uk

 

 

Received: 24 October 2022

Accepted: 18 November 2022

Published: 22 December 2022

 

Abstract: Non-Gaussian randomness widely exists in complex dynamical systems, in which the traditional mean-variance index cannot fully reflect the systematic characteristics. To improve the performance of control design subjected to non-Gaussian noises, stochastic distribution control (SDC) theory was proposed in the 1990s, where the output probability density function (PDF) has been investigated as an additional system variable. Following this framework, SDC has been extended to other research subjects in control systems such as filter design, fault diagnosis, and so on. It shows that SDC supplies an important solution to enhance the accuracy of system design, which is further beneficial to almost all the topics subject to non-Gaussian randomness. Meanwhile, the theoretical results of the SDC have been applied to several practical industrial applications. As data science raises based on the development of industrial artificial intelligence, SDC has been further developed recently focusing on data-driven design and multi-agent systems. To explore the new challenges with the evolution of SDC, e.g. unknown system models, unknown noise distributions, strong non-stationary transient dynamics, stability analysis and industrial applications, this survey summarises the most recent published results in the last 5 years of SDC work in terms of modelling, control, filtering, fault diagnosis, and industrial applications. Based on the technical analysis, potential future work is discussed in the end.

Keywords:

stochastic distribution control minimum entropy control minimum entropy filtering full probabilistic design data-driven design fault diagnosis performance enhancement non-gaussian stochastic systems

1. Introduction

Stochastic systems theory is an essential topic in system science regarding modelling, control, approximation, optimisation, and others. Traditionally, the Gaussian distribution is pre-assumed to simplify the formulation and it is suitable for most of the practical cases due to the central-limit theory. As a result, most of the research work focused on the mean-value and the variance control, where the two parameters are enough to characterise the Gaussian distribution properly. However, the Gaussian distribution assumption will fail for the strong nonlinear systems as the nonlinearities will change the shape of the distribution into a non-Gaussian format. Nowadays, the non-Gaussian randomness becomes visible in many processes due to the increase in systematic complexity. In this situation, the mean-value and the variance are no longer capable to represent the full probabilistic information. To deal with the non-Gaussian properties, it is significant to investigate non-Gaussian stochastic systems theory and its applications.

The stochastic distribution control was presented to address the non-Gaussian distribution regulation for dynamic systems. In particular, the B-spline Neural Networks have been used to re-present the output probability density function which means that the full probabilistic information of the system output can be described and then adjusted driven by the designed control input. Following this framework, various types of neural networks have been adopted to re-express the dynamics of the system variables and a series of results have been developed regarding control, filter, fault diagnosis and industrial applications. Some of the milestones have been reviewed and summarised in published survey reports [1, 2], which are omitted in this study.

Data science is becoming more relevant in computer science and engineering as a result of the development of machine learning. In other words, many engineering systems have been re-analysed from the point of the view of data. It implies that the data-driven design strongly influences the stochastic systems theory including almost all the aspects. At the same time, new challenges appear as the new design objectives of the stochastic systems, where the results based on the original SDC framework would not be transformed to solve the new problems. In particular, the main challenges can be summarised as follows.

1. The distribution of random noise is unknown. For some rigid-body motion mechanisms, accurate modelling can be achieved. Thus, the real-time output probability density function can be formulated using the system model and the noise distribution. Then, the control design and optimisation for the stochastic distribution are able to be achieved. However, in practice, it is impossible to model the random noise separately. It means that the noise distribution is unknown for most of the practical applications. To simplify the analysis, the Gaussian assumption is adopted to be the initial condition of the noise distribution, but this assumption cannot always be satisfied for industrial processes.

2. The system model is unknown. As mentioned above, the majority of real-world systems cannot be modelled accurately. Some systems cannot even acquire the model from the first principles due to the increasing complexity of system design. In such case, the output probability density function can only be numerically estimated by the collected data, which leads to the function fitting error. It has been shown that the error would affect the performance of the system design in terms of robustness. Even if the system model can be established by the data, the indirect probability density function control still suffers from the model fitting error. However, model fitting is out of the scope of this survey.

3. The transient nonlinear dynamics is not a stationary process. The systems normally contain nonlinear dynamics. Thus, the system probability density function will change within a short time if the system responses are rapid. In this case, it is difficult to obtain a sufficient amount of data to re-establish the distribution. Alternatively, Monte Carlo methods can be used to collect the simulated data in parallel. However, the computational workload will increase at the same time, meanwhile, the accuracy of the system model cannot be guaranteed.

4. Stability analysis is still an open question for data-driven design. Regarding the unknown system model and the strong transient dynamics, the theoretical stability analysis is a challenge. The existing SDC framework converts the system dynamics and represents the dynamics using the transformed dynamics of probability density functions. Thus, the control design is based on the obtained transformed model. In other words, stability is achievable if the equivalence of the model transformation can be guaranteed. For the closed-loop output stability, it is necessary to update the theoretical foundation.

5. Industrial applications would be affected by all the aforementioned factors. Basically, the cost and safety of the system design would be considered as priority. SDC would increase the computational cost, while the modelling and estimation fitting error would influence the performance of the practical processes. A simplified technical approach would be beneficial for large-scale industrial applications if the performance guarantee is attainable.

Recently, a lot of scholars made great improvements to address the aforementioned challenges and some of the results have achieved the design requirements while the problems were partly resolved. In this study, we summarise the main research work regarding non-Gaussian stochastic systems in the last 5 years and the survey structure is given in Figure 1. In particular, the stochastic distribution control problem is reviewed in Section 2. Section 3 summarises the results of minimum entropy systems. In Section 4, non-Gaussian filtering has been considered including the estimation, fault diagnosis, performance evaluation, performance enhancement, etc. And Section 5 indicates the advances in industrial applications subjected to non-Gaussian randomness. Moreover, the algorithm complexity has been indicated in Section 6. Based upon all these results, Section 7 discusses the potential directions for future work which concludes this survey.

Figure 1. Survey structure with the summarised sub-topics.

2. Probability Density Function Control

SDC can be considered as a type of probability density function regulation problem, shown in Figure 2 . Suppose that the desired probability density function is time-invariant and known. Thus, the design objective is to adjust the system probability density function to track the pre-specified one. It implies that the objective can be achieved once the distance between the given PDF and the concerned variable’s actual PDF is minimised. Thus, the critical formulation is to describe the distance as a cost function for controller design. The main challenge has been reflected in the unknown model of the system and the noise distributions. Data-driven SDC can solve the unknown issues. However, the estimation of PDF needs extra time, which will affect the stability and the accuracy if the process transient dynamics are strongly non-linear.

Figure 2. Block diagram of general probability density function (PDF) control.

2.1. Full Probability Design using Kullback-Leibler (KL) Divergence

To present the difference between the desired PDF and the concerned variable’s PDF, KL divergence can be selected as a cost function. Thus, the control signal can be evaluated to minimise the formulated KL divergence. Following this framework, Randa Herzallah and Yuyang Zhou have published a series of contributions in recent years. In particular, the PDF tracking control has been investigated for stochastic systems with input delay in [3, 4]. To extend this result, the PDF tracking has been achieved for stochastic systems with both input delay and state delay in [5]. As another benefit of KL divergence, the model constraint has been further released where the multiplicative noise systems were investigated following this framework [6, 7]. The framework is extended to message passing algorithm for complex networked systems using the decentralised design [8, 9]. Furthermore, the message passing control framework was proposed in [10] for a class of stochastic switching systems. For full probability design algorithms, the results focus on the optimisation of the KL-divergence, the system stability and error convergence have not been theoretically analysed.

2.2. PDF Control with Euclidean Distance

Although the cost function can be formed using KL divergence, it is not a standard metric as it is not symmetry. Therefore, Euclidean distance can be adopted to characterise the PDFs’ differences directly. In particular, Liping Yin has developed the PDF-based data-driven operational control framework using Euclidean distance [11]. Moreover, the Pareto optimisation method was merged into the framework for optimal operational control in [12]. In these results, the integral of the functions cannot be ignored. To reduce the computational complexity, Hong Wang and Qichun Zhang present a series of alternative descriptions. For example, [13] presents a vector-based converted distance metric to achieve data-driven PDF tracking control. Similarly, the data-driven PID controller was obtained based on the PDF vectorisation in [14]. To further simplify the expression of the distance, a histogram-based pseudo-state description has been developed using the Monte-Carlo simulation [15]. All the results mentioned in this sub-section are given with convergence analysis.

3. Minimum Entropy Optimisaiton

In practice, the desired PDF is not always available, and the main task of the control system is to attenuate the randomness of the system. Therefore, we can consider the PDF regulation as an optimisation problem. Since a sharper PDF shape typically equals less randomness, we specifically aim to alter the shape of the actual PDF as sharply as we can. The conventional method used minimal variance to sharpen the PDF due to the Gaussian assumption. As we previously stated, variance, however, is unable to describe the randomness of non-Gaussian distributions. For non-Gaussian cases, entropy from information theory is employed as a measurement of randomness. As a result, minimum entropy control was proposed to replace the minimum variance control for non-Gaussian systems and the general framework is shown in Figure 3 . The main challenge is similar to the aforementioned challenge for SDC, as entropy optimisation is an extension of the SDC framework.

Figure 3. Block diagram of general minimum entropy control.

3.1. Minimum Entropy Control

Based on the kernel density estimation, the entropy of the investigated system variable can be approximated using the collected data. [16] presents a novel data-driven approach to achieve the minimum entropy using cumulant-generating function. Similarly, a data-driven minimum entropy control algorithm was brought up by Yunlong Liu [17] using Taylor’s expansion of the performance criterion. Based on the system model, minimum entropy control can be achieved using disturbance observer [18]. In addition, the entropy index can be particularly replaced by various types of entropies, such as (h, phi)-entropy [19], correntropy [20]. Motivated by the information theory, the performance criterion can also be described by information potential, which can be estimated by data and equivalent to entropy regarding the randomness attenuation, such as the survival information potential [21]. Technically, the entropy metric cannot be solely used due to the entropy invariant property of PDF shifting. As a result, the mean-value is always added to the entropy performance criterion. Using information potential to replace entropy is one of the solutions to consider the influence of mean-values. Combining the information-theoretic learning technique, the composite anti-disturbance control was given for non-Gaussian stochastic systems in [22], where the hybrid control implementation is realised via the batch-to-batch mode through entropy optimisation and a disturbance observer. Note that all the results mentioned in this sub-section are given with stability analysis.

3.2. Continuous-Time Non-Gaussian Stochastic Systems Design

Most of the existing results focused on the discrete-time model as the data can be collected and considered as a random sequence, which simplified the controller design procedure. However, the discretisation would lose some basic information of the investigated systems. In other words, the full information and the stochastic properties should be described by the continuous-time system model, where the variables are treated as stochastic processes. So far, only a few results have been developed. For example, [23] presented an output feedback stabilisation problem with entropy optimisation for the Ito process model while the entropy assignment problem has been solved analytically for a class of nonlinear continuous-time stochastic systems in [24]. So far, it is still an open question for solving the general continuous-time stochastic differential equation and only some special types of equations have been investigated.

4. Filtering and Performance Enhancement

Based on the scheme of minimum entropy, a novel filter design strategy can be obtained by minimising the entropy value of the estimation error, shown in Figure 4 . Note that the error can be produced by both model-based filter design, data-based filter design and hybrid approach. Once the non-Gaussian filtering is implemented for non-Gaussian stochastic system, some related topics can be extended following the system monitoring and approximation, such as fault diagnosis and tolerance, performance evaluation and enhancement. The main challenge of non-Gaussian filtering has been summarised as the unknown noise distributions even if the model is obtained. Data-driven hybrid mode can re-establish the unknown estimation error dynamics. Similarly, data-based estimation needs extra time which also affects the stability and the accuracy of the filter design.

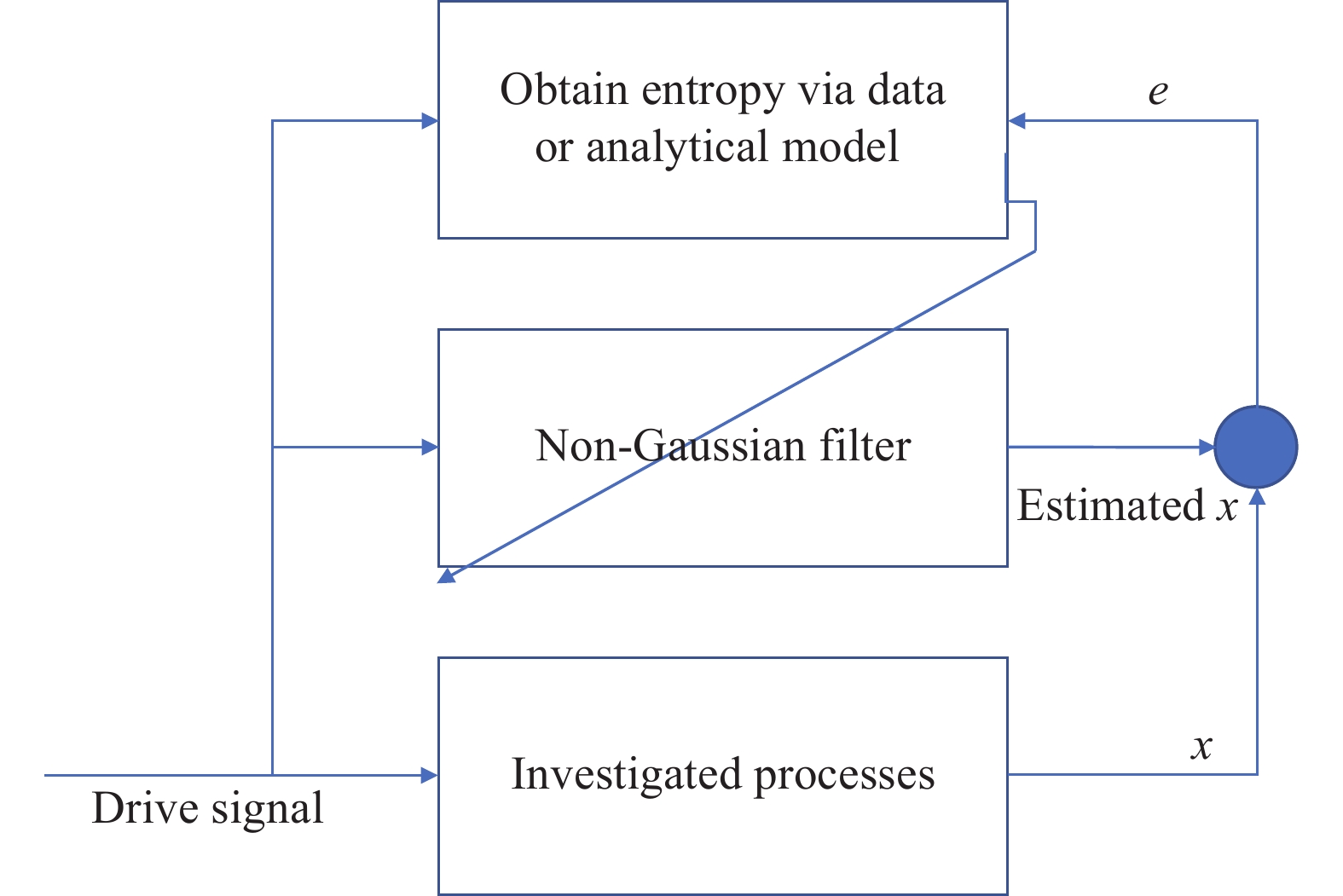
Figure 4. Block diagram of general entropy-based filtering.

4.1. Non-Gaussian Filter Design

Motivated by the minimum entropy optimisation, Lei Guo and his team have developed a series of filtering algorithms to deal with the estimation problem subjected to non-Gaussian noises. In particular, [25] presented a novel filtering scheme combining the particle filter and minimum entropy metric. Similarly, combining robust particle filtering, the non-Gaussian filter has been designed for a class of stochastic systems with time-varying model uncertainty and inaccurate noise covariance matrix [26]. Xin Yin developed a neural network based non-Gaussian filtering algorithm where the estimation error dynamics have been reconstructed for entropy value prediction [27]. In [28], the state estimation problem was investigated using the backstepping design for continuous-time stochastic systems. In practice, the Kalman filter is still applied as the most common design tool. Thus, [29] has proposed an approach to upgrade the Kalman filtering framework with the minimum entropy criterion.

Maximum correntropy-type filtering is another widely used design approach. [30-31] presented a fractional-order correntropy adaptive filter for -stable signals. [32] investigated the large-scale integration architecture for fractional-order correntropy adaptive filtering. Combining kernel estimation, the adaptive kernel size problem has been solved for the Kalman filter with maximum correntropy criterion [33]. In addition, the maximum correntropy criterion can be further generalised which leads to the new results using generalised maximum correntropy-type filtering design. The generalised maximum correntropy criterion has been adopted to kernel algorithms in [34-35], which can be potentially extended to data-driven non-Gaussian filtering. [36] further extended the kernel algorithms with variable kernel width. Various constrained generalised maximum correntropy filtering algorithms have been developed in [37-39]. Robustness as an important property for the filtering problem has been considered in [40-41] to enhance the performance of generalised maximum correntropy filters. Moreover, generalised maximum correntropy is beneficial to distributed estimation over networks [42].

The non-Gaussian filtering can also be achieved following the -distribution model. For example, the recursive estimation was obtained via the -distribution-based design approach in [43] and the robust generalised -distribution based Kalman filter was proposed in [44], and the proposed approach can be further extended to multi-sensor systems with heavy-tailed noises [45]. As examples of the practical application, -distribution based filtering has been involved in autonomous underwater vehicles [46] and manned aircrafts [47]. Robust filter design can also be implemented following variational Bayesian inference [48]. Noting the link between Bayesian inference and -distribution, the inference can be designed following Student-  Mixture Distributions [49].

In this sub-section, the convergence of the filtering algorithms has been considered. However, some of the results focused on optimisation and recursive kernel algorithms. The analysis is about function convergence and the analysis can be converted to error convergence for filtering problems.

4.2. Fault Diagnosis for Non-Gaussian Systems

For non-Gaussian stochastic systems, the monitoring can be implemented once the unmeasurable states are obtained through the presented filtering schemes, and this leads to updates for fault diagnosis and tolerant control. In particular, Lina Yao and her team consistently focus on this topic. Based on minimum entropy, [50] designed an active fault tolerant control strategy for non-Gaussian stochastic distribution systems with mean constraints. [51] presented the non-Gaussian fault tolerant control (FTC) for singular stochastic distribution systems using TS fuzzy modelling techniques. Furthermore, [52] investigated the fault diagnosis for non-Gaussian stochastic systems via entropy optimisation. Other contributions were also impressive, while the adaptive minimum entropy hybrid compensation method has been given for fault-tolerant design in [53]. In terms of sensor faults, the generalised correntropy filter has been applied to achieve fault diagnosis and tolerant control [54]. Regarding the system delay, fault detection and diagnosis were implemented using output PDFs for the delay-range-dependent stochastic systems in [55]. The methods use filtering approach and PDF control framework which are inherited stable.

4.3. Performance Enhancement

As the randomness can be attenuated using the minimum entropy design, the performance of the closed-loop control systems is able to be further enhanced following the optimisation strategy. Basically, rational entropy can be used to assess the performance of various control designs for non-Gaussian stochastic systems [56]. [57] carried out an EKF-based cooperation optimisation for stochastic nonlinear systems, where the system set-point can be dynamically adjusted following the minimum entropy criterion. In [58] a probabilistic decoupling design was proposed to enhance the multi-variable systems’ performance where the investigated nonlinear uncertain systems are subjected to non-Gaussian noises. A neural network driven compensation scheme has been produced to enhance the closed-loop system’s performance, where the additional information from the unmeasurable states can be re-involved in the controller design [59]. With the designed compensators, the closed-loop performance has been enhanced with guaranteed error convergence.

5. Industrial Applications

This section is a response to Challenge 5 in Introduction. Using these recent theoretical results regarding non-Gaussian stochastic systems, several industrial applications have been demonstrated in engineering fields. In this session, outstanding practical implementations are given to illustrate the power of the developed strategies. In particular, Jianhua Zhang has applied the minimum entropy algorithm to deal with the engineering challenges. For example, the polymerisation process [60] has been controlled from the view of the distribution using the moment-generating function. [61] investigates the future grid using decentralised fully probabilistic designed algorithms. [62] and [63] faced heavy industrial processes and applied PDF control algorithms to optimise the applications. In the refining process [64], the fibre length stochastic distribution has been shaped using data-driven predictive PDF control. In addition, the entropy-based iterative learning can be adopted for neuroscience, where the neural membrane mutual coupling characterisation has been completed by identifying the coupling factors [65].

6. Algorithm Complexity

Although the aforementioned algorithms have been illustrated with stability and convergence analysis. The complexity analysis is another key point for the system design topic, especially for the data-driven approach. For the traditional model based design, the system model can be established before the real-time operation. In other words, the control law can be calculated through the model without internal iteration and the complexity of the algorithm can be considered as . For the numerical solution searching approach, such as gradient optimisation, Riccati equation, etc., the complexity depends on the threshold and the step setting. For the recent data-driven approach, the estimation or modelling process is involved in each time instant, which means that numerical iteration affects the complexity in the loop. For example, the data-driven approach using kernel density estimation would be complex regarding the kernel number. It can be denoted as  with  kernel functions. In addition, some of the results contain a system identification procedure as the data structuring will extract the information from the investigated process. For system identification, the complexity depends on the number of system model parameters. For instance, [13] combined the least-square method, kernel density estimation and gradient descent algorithm, where the complexity analysis should be given separately and summed together in the end for the entire system design. Similarly, the neural network based design would contain high-complexity as the iteration occurs in each layer. As a dual problem, the filtering algorithm analysis is similar to the control design. Generally, the data-driven design will increase the algorithm complexity compared with the model-based design.

7. Perspectives and Future Work

With the rapid developments of data science and networked systems, the non-Gaussian properties will be visible in many complex systems, which would affect the system-level performance. In other words, the non-Gaussian stochastic systems theory will become more and more important along with the increase of the system's complexity. The following systems would be the potential focal points both in theory and in applications:

1. Distributed Networked Systems: Distributed Networked Systems [ 66 ] contain complex system dynamics and the interactions between sub-systems would bring unpredictive uncertainties into the transient dynamics. Therefore, the non-Gaussian framework will be beneficial to enhance the performance of the systems to reduce the randomness.

2. Deep Randomised Neural Networks: Neural networks theory generates significant impacts now with the rise of machine learning, especially deep learning. However, the parametric optimisation for model training remains a challenge for multi-layer structures. Thus, randomised learning [ 67 ] has been introduced into deep neural networks to speed up the training progress. By combining with the non-Gaussian features, the present randomised neural network learning theory could be expanded to improve modelling accuracy.

3. Robotics Teleoperation and Path Planning: Robotics systems have been widely used for many application scenarios, such as intelligent manufacturing, extreme environment detection, rescue, etc. For safety propose, robotics teleoperation [ 68 ] is necessary for practice. However, due to the communication and human-machine interaction, non-Gaussian randomness always has an effect on real-time performance. To enhance the quality of the teleoperation, the non-Gaussian stochastic system theory would attenuate the uncertainties in communication. In addition, the path planning of the robot is another application for entropy design as the decision-making would rely on the principle of entropy maximisation.

In summary, the non-Gaussian stochastic systems have been widely developed in many aspects, such as modelling, control, filtering, fault diagnosis, performance enhancement, and so on in the last 5 years. Meanwhile, the non-Gaussian stochastic systems have shown great potential in many important industrial processes and future work would inspire more scholars to solve the aforementioned challenges.

Author Contributions: Qichun Zhang: writing — original draft preparation; Yuyang Zhou: writing — review and editing; All authors have read and agreed to the published version of the manuscript.

Funding: This research received no external funding.

Conflicts of Interest: The authors declare no conflict of interest.

References

  1. Ren, M.F.; Zhang, Q.C.; Zhang, J.H, An introductory survey of probability density function control. Syst. Sci. Control Eng., 2019, 7: 158−170. DOI: https://doi.org/10.1080/21642583.2019.1588804
  2. Wang, A.P.; Wang, H, Survey on stochastic distribution systems: A full probability density function control theory with potential applications. Opt. Control Appl. Methods, 2021, 42: 1812−1839. DOI: https://doi.org/10.1002/oca.2755
  3. Herzallah, R, A fully probabilistic design for tracking control for stochastic systems with input delay. IEEE Trans. Autom. Control, 2021, 66: 4342−4348. DOI: https://doi.org/10.1109/TAC.2020.3032091
  4. Herzallah, R, A fully probabilistic design for stochastic systems with input delay. Int. J. Control, 2021, 94: 2934−2944. DOI: https://doi.org/10.1080/00207179.2020.1742386
  5. Herzallah, R.; Zhou, Y.Y, A fully probabilistic control framework for stochastic systems with input and state delay. Sci. Rep., 2022, 12: 7812. DOI: https://doi.org/10.1038/s41598-022-11514-z
  6. Herzallah, R.; Zhou, Y.Y, A tracking error–based fully probabilistic control for stochastic discrete-time systems with multiplicative noise. J. Vib. Control, 2020, 26: 2329−2339. DOI: https://doi.org/10.1177/1077546320921608
  7. Zhou, Y.Y.; Herzallah, R, DOBC based fully probability design for stochastic system with the multiplicative noise. IEEE Access, 2020, 8: 34225−34235. DOI: https://doi.org/10.1109/ACCESS.2020.2974279
  8. Herzallah, R.; Zhou, Y.Y. An efficient message passing algorithm for decentrally controlling complex systems. Int. J. Control 2021, in press. doi:10.1080/00207179.2021.2011422 DOI: https://doi.org/10.1080/00207179.2021.2011422
  9. Zhou, Y.Y.; Herzallah, R, Probabilistic message passing control and FPD based decentralised control for stochastic complex systems. AIMS Electron. Electr. Eng., 2020, 4: 216−233. DOI: https://doi.org/10.3934/ElectrEng.2020.2.216
  10. Zhou, Y.Y.; Herzallah, R, Probabilistic message passing control for complex stochastic switching systems. J. Franklin Inst., 2021, 358: 5451−5469. DOI: https://doi.org/10.1016/j.jfranklin.2021.04.040
  11. Lai, L.L.; Yin, L.P.; Hong, Y.; et al, Data driven optimal control for stochastic systems with non-Gaussian disturbances. Int. J. Modell. Identif. Control, 2021, 39: 245−256. DOI: https://doi.org/10.1504/IJMIC.2021.123493
  12. Yin, L.P.; Wang, H.; Guo, L.; et al, Data-driven Pareto-DE-based intelligent optimal operational control for stochastic processes. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 4443−4452. DOI: https://doi.org/10.1109/TSMC.2019.2936452
  13. Zhang, Q.C.; Wang, H, A novel data-based stochastic distribution control for non-Gaussian stochastic systems. IEEE Trans. Autom. Control, 2022, 67: 1506−1513.
  14. Liu, Y.F.; Zhang, Q.C.; Yue, H, Stochastic distribution tracking control for stochastic non-linear systems via probability density function vectorisation. Trans. Inst. Meas. Control, 2021, 43: 3149−3157. DOI: https://doi.org/10.1177/01423312211016929
  15. Zhang, Q.C.; Wang, H, Probability density function control for stochastic nonlinear systems using Monte Carlo simulation. IFAC-PapersOnLine, 2020, 53: 1288−1293. DOI: https://doi.org/10.1016/j.ifacol.2020.12.1857
  16. Zhang, Q.C.; Zhang, J.H.; Wang, H. Data-driven minimum entropy control for stochastic nonlinear systems using the cumulant-generating function. IEEE Trans. Autom. Control 2022, in press. doi:10.1109/TAC.2022.3208170
  17. Liu, Y.L.; Wang, A.P.; Guo, L.; et al, An error-entropy minimization algorithm for tracking control of nonlinear stochastic systems with non-Gaussian variables. IFAC-PapersOnLine, 2017, 50: 10407−10412. DOI: https://doi.org/10.1016/j.ifacol.2017.08.1720
  18. Tian, B.; Wang, Y.; Guo, L, Disturbance observer-based minimum entropy control for a class of disturbed non-Gaussian stochastic systems. IEEE Trans. Cybern., 2020, 52: 4916−4925. DOI: https://doi.org/10.1109/TCYB.2020.3024997
  19. Zhang, J.H.; Pu, J.Z.; Lin, M.M.; et al, Superheating control of ORC systems via minimum (h,φ)-entropy control. Entropy, 2022, 24: 513. DOI: https://doi.org/10.3390/e24040513
  20. Ren, M.F.; Gong, M.Y.; Lin, M.M.; et al, Generalized correntropy predictive control for waste heat recovery systems based on organic rankine cycle. IEEE Access, 2019, 7: 151587−151594. DOI: https://doi.org/10.1109/ACCESS.2019.2948284
  21. Yin, L.P.; Lai, L.L.; Zhu, Z.J.; et al, Maximum power point tracking control for non-Gaussian wind energy conversion system by using survival information potential. Entropy, 2022, 24: 818. DOI: https://doi.org/10.3390/e24060818
  22. Tian, B.; Wang, C.L.; Guo, L, Composite Antidisturbance control for non-Gaussian stochastic systems via information-theoretic learning technique. IEEE Trans. Neural Netw. Learn. Syst., 2022, 33: 7644−7654. DOI: https://doi.org/10.1109/TNNLS.2021.3086032
  23. Zhang, Q.C.; Hu, L.; Gow, J, Output feedback stabilization for MIMO semi-linear stochastic systems with transient optimisation. Int. J. Autom. Comput., 2020, 17: 83−95. DOI: https://doi.org/10.1007/s11633-019-1193-8
  24. Tang, X.F.; Zhou, Y.Y.; Zou, Y.Q.; et al, Variance and entropy assignment for continuous-time stochastic nonlinear systems. Entropy, 2022, 24: 25. DOI: https://doi.org/10.3390/e24010025
  25. Li, W.S.; Wang, Z.D.; Yuan, Y.; et al, Two-stage particle filtering for non-Gaussian state estimation with fading measurements. Automatica, 2020, 115: 108882. DOI: https://doi.org/10.1016/j.automatica.2020.108882
  26. Li, W.S.; Guo, L, Robust particle filtering with time-varying model uncertainty and inaccurate noise covariance matrix. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 7099−7108. DOI: https://doi.org/10.1109/TSMC.2020.2964325
  27. Yin, X.; Zhang, Q. C.; Wang, H.; et al, RBFNN-based minimum entropy filtering for a class of stochastic nonlinear systems. IEEE Trans. Autom. Control, 2020, 65: 376−381. DOI: https://doi.org/10.1109/TAC.2019.2914257
  28. Yin, X.; Zhang, Q.C, Backstepping-based state estimation for a class of stochastic nonlinear systems. Complex Eng. Syst., 2022, 2: 1. DOI: https://doi.org/10.20517/ces.2021.13
  29. Zhang, Q.C, Performance enhanced Kalman filter design for non-Gaussian stochastic systems with data-based minimum entropy optimisation. AIMS Electron. Electr. Eng., 2019, 3: 382−396. DOI: https://doi.org/10.3934/ElectrEng.2019.4.382
  30. Gogineni, V.C.; Talebi, S.P.; Werner, S.; et al, Fractional-order correntropy adaptive filters for distributed processing of α-stable signals. IEEE Signal Process. Lett., 2020, 27: 1884−1888. DOI: https://doi.org/10.1109/LSP.2020.3029702
  31. Gogineni, V.C.; Talebi, S.P.; Werner, S.; et al, Fractional-order correntropy filters for tracking dynamic systems in α-stable environments. IEEE Trans. Circuits Syst. II Exp. Briefs, 2020, 67: 3557−3561. DOI: https://doi.org/10.1109/TCSII.2020.2995357
  32. Alex, D.; Gogineni, V.C.; Mula, S.; et al, Novel VLSI architecture for fractional-order correntropy adaptive filtering algorithm. IEEE Trans. Very Large Scale Integr. VLSI Syst., 2022, 30: 893−904. DOI: https://doi.org/10.1109/TVLSI.2022.3169010
  33. Fakoorian, S.; Izanloo, R.; Shamshirgaran, A.; et al. Maximum correntropy criterion Kalman filter with adaptive kernel size. In Proceedings of 2019 IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 15–19 July 2019; IEEE: Dayton, 2019; pp. 581–584. doi:10.1109/NAECON46414.2019.9057886 DOI: https://doi.org/10.1109/NAECON46414.2019.9057886
  34. Zhang, T.; Wang, S.Y, Nyström kernel algorithm under generalized maximum correntropy criterion. IEEE Signal Process. Lett., 2020, 27: 1535−1539. DOI: https://doi.org/10.1109/LSP.2020.3019166
  35. Zhao, J.; Zhang, H.B, Kernel recursive generalized maximum correntropy. IEEE Signal Process. Lett., 2017, 24: 1832−1836. DOI: https://doi.org/10.1109/LSP.2017.2761886
  36. Zhao, H.Q.; Chen, B.; Zhu, Y.Y.; et al, Variable Kernel width algorithm of generalized maximum correntropy criteria for censored regression. IEEE Trans. Circuits Syst. II Exp. Briefs, 2021, 69: 1877−1881. DOI: https://doi.org/10.1109/TCSII.2021.3103504
  37. Sun, Q.; Zhang, H.; Wang, X.F.; et al, Sparsity constrained recursive generalized maximum correntropy criterion with variable center algorithm. IEEE Trans. Circuits Syst. II Exp. Briefs, 2020, 67: 3517−3521. DOI: https://doi.org/10.1109/TCSII.2020.2986053
  38. Zhao, J.; Zhang, J.A.; Li, Q.; et al, Recursive constrained generalized maximum correntropy algorithms for adaptive filtering. Signal Process., 2022, 199: 108611. DOI: https://doi.org/10.1016/j.sigpro.2022.108611
  39. Liu, D.X.; Zhao, H.Q.; He, X.Q.; et al, Polynomial constraint generalized maximum correntropy normalized subband adaptive filter algorithm. Circuits Syst. Signal Process., 2022, 41: 2379−2396. DOI: https://doi.org/10.1007/s00034-021-01878-4
  40. Zhu, Y.Y.; Zhao, H.Q.; Zeng, X.P.; et al, Robust generalized maximum correntropy criterion algorithms for active noise control. IEEE/ACM Trans. Audio Speech Lang. Process., 2020, 28: 1282−1292. DOI: https://doi.org/10.1109/TASLP.2020.2982030
  41. Bhattacharjee, S.S.; Shaikh, M.A.; Kumar, K.; et al, Robust constrained generalized correntropy and maximum versoria criterion adaptive filters. IEEE Trans. Circuits Syst. II Exp. Briefs, 2021, 68: 3002−3006. DOI: https://doi.org/10.1109/TCSII.2021.3063491
  42. Chen, F.; Li, X.Y.; Duan, S.K.; et al, Diffusion generalized maximum correntropy criterion algorithm for distributed estimation over multitask network. Digital Signal Process., 2018, 81: 16−25. DOI: https://doi.org/10.1016/j.dsp.2018.02.008
  43. Sun, L.; Ho, W.K.; Ling, K.V.; et al, Recursive maximum likelihood estimation with t-distribution noise model. Automatica, 2021, 132: 109789. DOI: https://doi.org/10.1016/j.automatica.2021.109789
  44. Bai, M.M.; Sun, C.J.; Zhang, Y.G, A ROBUST GENeralized t distribution-based Kalman filter. IEEE Trans. Aerosp. Electron. Syst., 2022, 58: 4771−4781. DOI: https://doi.org/10.1109/TAES.2022.3160984
  45. Yan, L.P.; Di, C.Y.; Wu, Q.M.J.; et al, Distributed fusion estimation for multisensor systems with non-Gaussian but heavy-tailed noises. ISA Trans., 2020, 101: 160−169. DOI: https://doi.org/10.1016/j.isatra.2020.02.004
  46. Li, Q.; Ben, Y.Y.; Naqvi, S.M.; et al, Robust student’s t-based cooperative navigation for autonomous underwater vehicles. IEEE Trans. Instrum. Meas., 2018, 67: 1762−1777. DOI: https://doi.org/10.1109/TIM.2018.2809139
  47. Youn, W.; Huang, Y.L.; Myung, H, Outlier-robust student's-t-based IMM-VB localization for manned aircraft using TDOA measurements. IEEE/ASME Trans. Mechatron., 2020, 25: 1646−1658. DOI: https://doi.org/10.1109/TMECH.2020.2982009
  48. Xu, C.; Zhao, S.Y.; Ma, Y.J.; et al, Robust filter design for asymmetric measurement noise using variational Bayesian inference. IET Control Theory Appl., 2019, 13: 1656−1664. DOI: https://doi.org/10.1049/iet-cta.2018.6016
  49. Zhang, T.Y.; Zhao, S.Y.; Luan, X.L.; et al. Bayesian inference for state-space models with student-t mixture distributions. IEEE Trans. Cybern. 2022, in press. doi:10.1109/TCYB.2022.3183104 DOI: https://doi.org/10.1109/TCYB.2022.3183104
  50. Jin, H.K.; Guan, Y.C.; Yao, L.N, Minimum entropy active fault tolerant control of the non-Gaussian stochastic distribution system subjected to mean constraint. Entropy, 2017, 19: 218. DOI: https://doi.org/10.3390/e19050218
  51. Li, L.F.; Yao, L.N, Minimum rational entropy fault tolerant control for non-Gaussian singular stochastic distribution control systems using T-S fuzzy modelling. Int. J. Syst. Sci., 2018, 49: 2900−2911. DOI: https://doi.org/10.1080/00207721.2018.1526984
  52. Yao, L.N.; Li, L.F.; Guan, Y.C.; et al, Fault diagnosis and fault-tolerant control for non-Gaussian nonlinear stochastic systems via entropy optimisation. Int. J. Syst. Sci., 2019, 50: 2552−2564. DOI: https://doi.org/10.1080/00207721.2019.1671535
  53. Hu, K.Y.; Chen, F.Y.; Cheng, Z.A.; et al, Adaptive minimum-entropy hybrid compensation for compound faults of non-Gaussian stochastic systems. IEEE Access, 2019, 7: 120695−120707. DOI: https://doi.org/10.1109/ACCESS.2019.2936100
  54. Xu, X.Y.; Zhang, Y.Y.; Ren, M.F.; et al, Generalized correntropy filter-based fault diagnosis and tolerant control for non-Gaussian stochastic systems subject to sensor faults. IEEE Access, 2018, 6: 12598−12607. DOI: https://doi.org/10.1109/ACCESS.2018.2800730
  55. Yin, L.P.; Zhu, P.W.; Li, T, Fault detection and diagnosis for delay-range-dependent stochastic systems using output PDFs. Int. J. Control Autom. Syst., 2017, 15: 1701−1709. DOI: https://doi.org/10.1007/s12555-016-0048-0
  56. Zhou, J.L.; Jia, Y.Q.; Jiang, H.X.; et al, Non-Gaussian systems control performance assessment based on rational entropy. Entropy, 2018, 20: 331. DOI: https://doi.org/10.3390/e20050331
  57. Tang, X.F.; Zhang, Q.C.; Hu, L, An EKF-based performance enhancement scheme for stochastic nonlinear systems by dynamic set-point adjustment. IEEE Access, 2020, 8: 62261−62272. DOI: https://doi.org/10.1109/ACCESS.2020.2984744
  58. Zhang, Q.C.; Yin, X, Observer-based parametric decoupling controller design for a class of multi-variable non-linear uncertain systems. Syst. Sci. Control Eng., 2018, 6: 258−267. DOI: https://doi.org/10.1080/21642583.2018.1483276
  59. Zhou, Y.Y.; Wang, A.P.; Zhou, P.; et al, Dynamic performance enhancement for nonlinear stochastic systems using RBF driven nonlinear compensation with extended Kalman filter. Automatica, 2020, 112: 108693. DOI: https://doi.org/10.1016/j.automatica.2019.108693
  60. Zhang, J.H.; Pu, J.Z.; Ren, M.F, Molecular weight distribution control for polymerization processes based on the moment-generating function. Entropy, 2022, 24: 499. DOI: https://doi.org/10.3390/e24040499
  61. Herzallah, R.; Zhou, Y.Y, Probabilistic decentralised control and message passing framework for future grid. Int. J. Electr. Power Energy Syst., 2021, 131: 107114. DOI: https://doi.org/10.1016/j.ijepes.2021.107114
  62. Zhang, Y.; Zhou, P.; Cui, G.M, Multi-model based PSO method for burden distribution matrix optimization with expected burden distribution output behaviors. IEEE/CAA J. Autom. Sin., 2019, 6: 1506−1512. DOI: https://doi.org/10.1109/JAS.2018.7511090
  63. Zhang, Y.; Zhou, P.; Lv, D.H.; et al, Inverse calculation of burden distribution matrix using B-spline model based PDF control in blast furnace burden charging process. IEEE Trans. Ind. Inf., 2023, 19: 317−327. DOI: https://doi.org/10.1109/TII.2022.3157641
  64. Li, M.J.; Zhou, P.; Liu, Y.L.; et al. Data-driven predictive probability density function control of fiber length stochastic distribution shaping in refining process. IEEE Trans. Automat. Sci. Eng. 2020, 17, 633–645. doi:10.1109/TASE.2019.2939052 DOI: https://doi.org/10.1109/TASE.2019.2939052
  65. Tang, X.F.; Zhang, Q.C.; Dai, X.W.; et al, Neural membrane mutual coupling characterisation using entropy-based iterative learning identification. IEEE Access, 2020, 8: 205231−205243. DOI: https://doi.org/10.1109/ACCESS.2020.3037816
  66. Zhang, X.M.; Han, Q.L.; Ge, X.H.; et al, Networked control systems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin., 2020, 7: 1−17. DOI: https://doi.org/10.1109/JAS.2019.1911651
  67. Pratama, M.; Wang, D.H, Deep stacked stochastic configuration networks for lifelong learning of non-stationary data streams. Inf. Sci., 2019, 495: 150−174. DOI: https://doi.org/10.1016/j.ins.2019.04.055
  68. Zhang, D.D.; Si, W.Y.; Fan, W.; et al, From teleoperation to autonomous robot-assisted microsurgery: A survey. Mach. Intell. Res., 2022, 19: 288−306. DOI: https://doi.org/10.1007/s11633-022-1332-5