Adaptive Dynamic Programming for Networked Control Systems under Communication Constraints: A Survey of Trends and Techniques

2.1. The Development of ADP Structures

Survey/review study

Adaptive Dynamic Programming for Networked Control Systems under Communication Constraints: A Survey of Trends and Techniques

Xueli Wang ¹, Ying Sun ^1,*, and Derui Ding ²

¹ Department of Control Science and Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

² School of Software and Electrical Engineering, Swinburne University of Technology, Melbourne 3122, Australia

^* Correspondence: yingsun1991@163.com

Received: 22 September 2022

Accepted: 28 November 2022

Published: 22 December 2022

Abstract: The adaptive dynamic programming (ADP) technology has been widely used benefiting from its recursive structure in forward and the prospective conception of reinforcement learning. Furthermore, ADP-based control issues with communication constraints arouse ever-increasing research consideration in theoretical analysis and engineering applications due mainly to the wide participation of digital communications in industrial systems. The latest development of ADP-based optimal control with communication constraints is systematically surveyed in this paper. To this end, the development of ADP-based dominant methods is first investigated from their structures and implementation. Then, technical challenges and corresponding approaches are comprehensively and thoroughly discussed and the existing results are reviewed according to the constraint types. Furthermore, some applications of the ADP method in practical systems are summarized. Finally, future topics are lighted on ADP-based control issues.

1. Introduction

In recent years, networked control systems (NCSs) have emerged with the consistent development of network technology, the innovation of computing methods, and the complex engineering requirements for systems with decentralized/distributed deployment [1]. The control performance of NCSs has also been greatly improved, benefiting from the development of analysis technics and various design methods. Generally speaking, the design of controllers for NCSs under different network-induced phenomena mainly considers the stability and robustness of industrial process control and is rarely concerned with the overall performance, cost as well as energy consumption. Furthermore, the nonlinearities are ubiquitous due mainly to the internal physical mechanism, complex subsystem coupling, and state-dependent disturbances. Most existing researches assume that nonlinear functions are bounded by a linear condition, such as set-bounded conditions and Lipschitz conditions. Such an assumption is difficult to reflect the essence of nonlinearity and the corresponding results are relatively conservative. Furthermore, the control cost could not meet the actual need. As such, on the premise of ensuring the stable operation of the network system, the optimal control of the NCSs attracts attention [2-4].

When optimal control is a concern, there exist three classical solution methods, that is, the calculus of variations, the maximum principle, and dynamic programming (DP). It should be pointed out that the calculus of variations is suitable for the optimal control of constraint-free systems. Both the maximum principle and DP can deal with the optimal control problem of the system under compact set limits. Among them, the calculus of variations leads to the maximum principle, and DP is essentially a method of mathematical programming. Furthermore, DP describes the optimal control of the system through a computer-solvable recursive function of multi-level decisions, which is usually equivalent to solving the Hamilton-Jacobi-Bellman (HJB) equation. Particularly, the DP method appears a fatal flaw in the optimal control of complex nonlinear systems, that is, the "curse of dimensionality" problem. To overcome such a shortage, adaptive dynamic programming (ADP) has been developed by Werbos in [5]. The method intelligently integrates the reinforcement learning conception and the DP and uses the universal approximation of neural networks (NNs) to transform the inverse order solution into a positive order process, thereby the computational burden and the requirement of storage capacity are definitely reduced [6-8].

Another important aspect is that communication networks in actual engineering systems universally serve as the medium of information interaction, and are commonly governed by various transmission control protocols (TCPs) to guarantee the reliability and efficiency of information transmission while preventing the conflict of data packages. According to scheduling mechanisms, protocols can be roughly divided into Round-Robin (RR) protocols [9-10], weighted try-once-discard (TOD) protocols [11], stochastic communication protocols (SCPs) [12-13] and event-triggered mechanisms (ETMs) [14]. The essential idea of these protocols is to economize on communication resources and improve communication efficiency by reducing the amount of data transmitted. It is worth mentioning that the system cannot obtain complete information in comparison with traditional control systems due mainly to integrated protocols, which inevitably damage system performances and meanwhile bring challenges to the solution of optimal control. In addition, the inherent limitation of channel bandwidth and the inherent vulnerability of shared networks [15-16] will lead to the occurrence of various network-induced phenomena, including, time delays (TD) [17], packet loss [18], signal quantizations [9, 19], as well as cyber-attacks [20-21], etc. For the above systems considering communication protocols as well as network-induced phenomena, the whole system state cannot be reliably received and hence the theoretical solution of HJB equations cannot be easily derived.

More specifically, there are the following unavoidable challenges when engaging in the innovative research of ADP-based control theories and their applications. (1) Due to the data sparsity and incompleteness caused by protocol scheduling, it becomes more difficult to establish the corresponding HJB equations [22] in theory to reflect and quantize their impact. (2) Compared with the traditional NCS, the performance of NCS with the network-induced phenomenon is bound to deteriorate, oscillate or even become unstable. These phenomena are usually uncertain and stochastic. As such, it is a challenging task to cope with these phenomena to meet the framework requirement of optimal control such that the ideal controller structure can be received. (3) Scheduling rules could dynamically change the internal topological relationship of subsystems. In this case, the traditional analysis fails to satisfy the control requirements. Therefore, it is worthwhile to carefully investigate how to effectively overcome such trouble brought by the changes in complex topology structures. In recent years, many researchers devote themselves to providing satisfactory answers by developing novel ADP algorithms for various networked systems. Up to now, there are some systematic surveys on ADP-based optimal control, including its structures, algorithms, applications, and the analysis of convergence performance, see [23-27]. Unfortunately, to the best of our knowledge, there still lacks a systematic and professional survey about the ADP-based control under communication constraints, which stimulates our investigation interest.

This survey systematically investigates and summarizes the latest development of ADP-based control for networked systems under communication constraints. First, the development of ADP-based dominant methods are investigated in Section 2, consisting of the structures in Subsection 2.1., and the algorithms in Subsection 2.2. Depending on the considered constraints, the survey is structured as follows. ADP based control latest development under communication constraints is profoundly introduced in Section 3, including ADP-based control with network-induced phenomena in Subsection 3.1. and one with communication protocols in Subsection 3.2. In what follows, the applications of the ADP-based control method in practical systems are systematically reviewed in Section 3.3. Finally, conclusions and future works are given in Section 4.

2. The Development of ADP Methods

Since it was proposed by Bellman in 1957 [28], the DP method has been attracting attention benefiting from its excellent role played in optimal control. The core of this method is just Bellman's optimal principle of the following property: for a multi-level decision-making process, the optimal strategy means that the rest of the decisions where the state is formed by the initial decision must be an optimal one for the initial state and decision. Now, let us take the following discrete-time nonlinear system as an example:

with  being a system state and  being a control strategy. The associate cost is employed as follows:

with  being the utility function,  is the discount factor satisfying . Based on the principle of Bellman optimality, the corresponding HJB equation is derived to be

The corresponding control strategy  at time  also reaches the optimum, denoted as

It is not difficult to find that the critical work of the design of optimal controllers is to solve the related HJB equation. However, the existence of the curse of dimensionality as well as the intrinsic nonlinear feature of such an equation makes it difficult to be solved. To overcome these obstacles, the framework of the ADP method has been first proposed in [5], and its implementation [29] has been realized by using some functional approximation structures (such as NNs, fuzzy models, and polynomials) to estimate the cost function. Furthermore, the solution to dynamic programming issues can be attained forward in time. The overall ADP structure comprises three parts: the system environment, actor/controller, and critic/performance index function, see Figure 1. In what follows, let us survey the development of ADP approaches in terms of their structure and algorithm in recent years.

Figure 1. The schematic diagram of ADP approaches.

Each part of the ADP framework in Figure 1 usually can be replaced by NNs, which are called the model NN, the actor NN as well as the critic NN. Specifically, NNs for models, actors, and critics are employed to approximate the system dynamics, the ideal optimal control strategy, as well as the optimal cost function, respectively. Based on the principle of Bellman optimality, the NNs' weights are updated iteratively via gradient descent rules to approximate the ideal value. The basic structures of ADP involve the well-known heuristic dynamic programming (HDP) and dynamic heuristic programming (DHP), see Figure 2 and Figure 3. Compared with these two frameworks, the main difference is that the critic NN in DHP is to approximate the gradient , while the one in HDP is used to approximate the cost  itself.

Figure 2. The structure of HDP approaches.

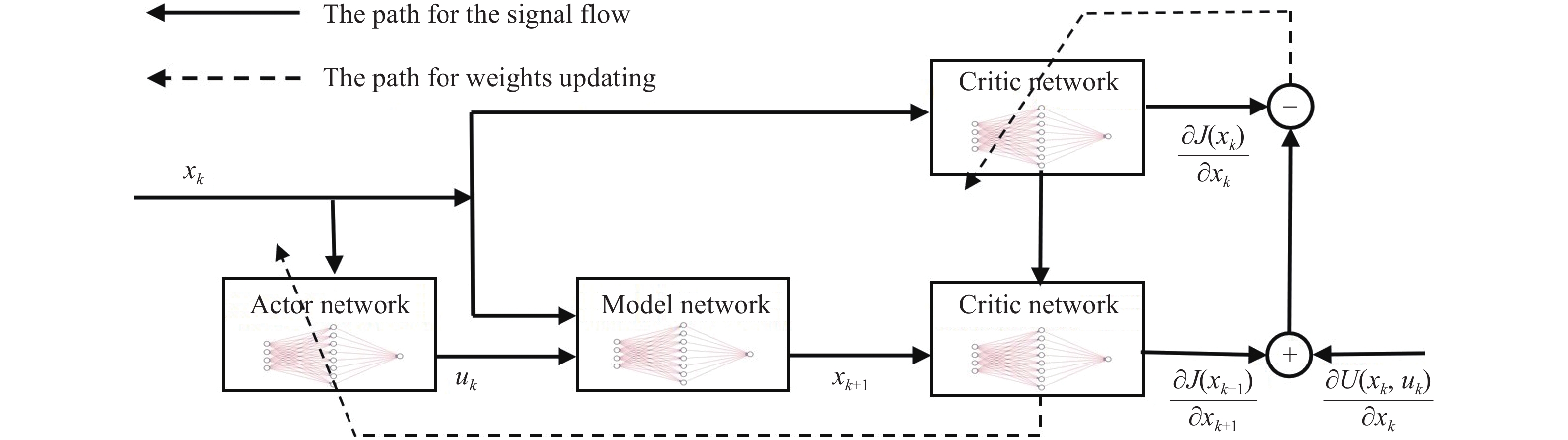
Figure 3. The structure of DHP approaches.

Inspired by the above two structures, various derivative structures have been proposed in light of the attempt of reducing the computational complexity and improving computational accuracy. For instance, the input of the critic NN in the action-dependent HDP (ADHDP) and action-dependent DHP (ADDHP) methods includes not only the system dynamic but also the control strategy in order to improve the calculation accuracy. On this basis, globalized DHP (GDHP) and action-dependent globalized DHP (ADGDHP) approaches have been developed in [26], and their typical is that the critic NNs simultaneously output the values of the estimated cost function and its gradient. Note that GDHP has a high approximation accuracy than ADGDHP by sacrificing computational speed. Furthermore, when the actor-critic structure is abandoned, a single network adaptive critic (SNAC) has been adopted in [30], where its output is the cost function or its gradient. This kind of critic-only framework can effectively improve the computational speed and reduce the approximation error, but the disadvantage is that it is unable to solve the optimal control problem of the non-affine control system. Subsequently, an improved version, named goal representation ADP (GrADP), has been found in [31], where its critic NN has the capability of adaptive adjustment of reward/punishment signals related to the system dynamics and control inputs, thereby improving the approximate accuracy. Through the combination of sparse kernel machine learning and ADP structures, a kernel-based ADP structure has been constructed in [32] to enable the traditional ADP algorithm to have both generalization and approximation capabilities.

2.2. The Development of ADP Algorithms

It is very challenging to solve the analytical solution of the famous HJB equation. Over the last few decades, various effectual ADP-based algorithms constantly come out with the joint efforts of scholars from control and mathematical societies. According to their iterative strategies, these algorithms can be roughly divided into off-line learning algorithms and online learning algorithms, and the corresponding stability and convergence analysis have also received great research attention.

2.2.1. Off-Line Learning Algorithms

The offline learning algorithm possesses an iterative calculation format to approximate the optimal control strategy. In line with the order of control strategies and cost/value function iteration, it can be further divided into policy iteration (PI) and value iteration (VI). Among them, the initial condition in PI needs to be selected from an allowable control set. Such a control law is substituted into the iterative HJB equation for evaluation, and the current value function is obtained simultaneously. Then, the strategy will be updated based on the received cost. Furthermore, the two steps of evaluation and update are carried out repeatedly until the termination condition is satisfied. Its pseudo-code can be found in Algorithm 1. Other than PI algorithms, VI algorithms are any given initial positive cost, and the pseudo-code is presented in Algorithm 2. Similarly, the expectant control strategy is finally obtained through continuous iteration. Obviously, in comparison with VI, PI algorithms can quickly find the optimal control strategy benefiting from the requirement of initial allowable control conditions.

Both the PI algorithm and the VI algorithm have been widely used, and their stability and convergence have been discussed in [33]. Very recently, the robustness of PI algorithms except the stability has also been discussed in [34] for continuous-time (CT) infinite-horizon linear systems. The convergence of a model-based bias-PI method has been rigorously proved in [35] for the data-based ADP control of unknown CT linear systems. Furthermore, a relaxation factor inspired by reinforcement learning has been exploited in [36] to guarantee the convergence of VI algorithms by regulating the rate of convergence for value function sequences.

2.2.2. Online Learning Algorithms

Different from the offline ones, the online learning algorithms mean that the control strategy and the value function will be adjusted synchronously over time [37-38]. In other words, the central theme is that online parametric structures (such as NNs, and fuzzy rules) are utilized to approximate the expected cost and the control input with the help of current and recorded system data. It should be pointed out that the iteration update is synchronous with the dynamic evolution of systems, which is different from the strategies in Algorithm 1 and Algorithm 2 in that 1) the training data is collected at the same instant, and 2) the iteration update is completed yet independent of the dynamic evolution of systems. As such, the main merit of this kind of algorithm can dynamically adjust to conform to the changes in system parameters.

With the help of the execution evaluation framework, an online learning algorithm has been employed to obtain the ideal control strategy of isolated subsystems, and then applied such a strategy to realize the design of decentralized controllers so that the entire interconnected system reaches stability in [39]. On the basis of this classic method, an online adaptive learning algorithm has been proposed in [37] to carry out the infinite domain ADP control problem of continuous systems. Note that the online learning algorithms are usually based on a well-known persistence excitation (PE) via an appropriate probe noise to stabilize the addressed systems. Such a requirement can be relaxed via experience replay techniques. For instance, the experience replay technique has been creatively utilized to effectively handle the event-based control issue without system dynamics in the framework of multi-player games [40]. Furthermore, concurrent learning, a kind of typical technique that effectively avoids PE conditions, has been provided in [41] to update NNs' weights. Using historical data, an event-based ADP controller has been designed to ensure the robustness of uncertain systems.

3. The ADP Control under Communication Constraints for Networked Systems

The latest development of ADP control under communication constraints will be elaborated in this section.

3.1. ADP Control with Network-Induced Complexities

In light of the vulnerability of shared networks and the limitation of channel bandwidth, network-induced scenes will inevitably occur, such as network attacks, TD, packet loss, as well as quantization, which threaten the security, stability, and reliability of practical NCSs. Thus, it is essential to develop a resilient ADP controller to ease the impact of these non-ideal data.

3.1.1. ADP Control with Network-Induced Phenomena

In networked systems, the interaction between devices and controllers is usually connected by converting analog and digital signals to quantify the signal and complete the device connection [42]. As the quantization phenomenon is unavoidable in NCSs, more and more designed controllers, involving ADP ones, adequately consider the influence of information quantization. For instance, an online NN observer has been designed in [43] to estimate both the system dynamics and the system parameter while eliminating the influence of quantization errors. At the same time, a similar dynamic quantization technique has also been utilized in [44] to deal with optimal control problems for the uncertain linear time-varying discrete-time (DT) systems. Since the system state is time-dependent in the finite horizon, an adaptively online estimator in the framework of ADHDP has been adopted to learn the constructed cost with time-varying natures, and a supplementary error term is introduced to describe the constraint at the end of time. Furthermore, the hysteresis quantizer reducing the oscillation has been investigated in [45] where the structure of ADP-based controllers involves a nonlinear part via NN forms and a linear part reflecting the tracking errors. The output of hysteresis quantizers is dependent on both the input and its rate of change and can be rewritten as the inputs plus a constrained unknown term. According to such a controller structure, the critic’s function comprises a Sigmoid-type vector and a nonlinear vector generated by NNs.

The TD is an inherent feature of information transmission, which could result in the performance degradation of NCSs. For example, due mainly to network TDs, which maybe reduce the speed and effectiveness of power control of wind turbines, a TD exists inevitably in the hydraulic pitch actuator. As such, it is of great significance how to overcome the difficulties caused by TDs, such as system instability, and degradation of other required control performances. To this end, some interesting attempts have been performed under the ADP framework. Note the fact that a class of time-delayed linear systems own the equivalence relationship with the delay-free system. Such an equivalence transformation eliminates the time-delay form, making the system to be addressed easily, and has been employed in [46] to discuss a model-free optimal control issue. Furthermore, the equivalent condition of multiple delayed systems and delay-free systems has been derived via the property of the system with TDs in [47]. Considering the difference of delay orders in equivalent multiple TD systems, they presented a new data-based dynamic equation dependent on historical data to overcome the challenge of the unmatched dimensions of the system dynamics. Very recently, the data-based ADP approach has been inventively provided to address the  tracking control problem for TD linear systems in [48], where such a problem has been converted into a zero-sum game.

When the optimal control of multi-agent systems is considered, the effect of multiple TDs cannot be ignored. In this regard, necessary and sufficient conditions of equivalent multi-TD systems have been derived to ensure the control performance of the system through a typical causal transformation method in [49], and the data-driven ADP algorithm has been developed by transforming optimal tracking into settling of the Nash-equilibrium in the graphical game. For nonlinear systems with TDs, the augmented technology, that is, stacking all TD-based states or inputs into an entirety, is applied to transform the corresponding system into a general nonlinear one of unknown dynamics. For instance, the ADP-based controller has been developed for nonlinear uncertain systems with TDs in [50]. In other words, the gradient descent method is used to update the weight of the NN, so that the designed NN adaptively approximates the control rate, and the closed-loop system is proved to realize the uniformly ultimate boundedness. In summary, it is found that the key to solving these ADP-based control problems is to bypass the challenges of TDs by a TD to non-TD transformation.

In an actual system, due to network congestion, node competition failures, packet collision, or channel interference, it is possible that the number of data arriving at the endpoint does not match that transmitted by the transmitter. All these phenomena are considered to be the loss of network data, that is, packet loss or packet dropouts [18, 51-52]. A core task of optimal control problems, suffering from packet loss, is to design an optimal controller that minimizes performance metrics and tolerates data acquisition failures for the controller-to-actuator and sensor-to-controller channels while guaranteeing the stability of resulting closed-loop systems [53]. In the absence of a priori knowledge of partial system dynamics and probabilities of packet dropouts, two reinforcement-learning-based online PI and VI algorithms have been developed to approximately calculate the optimal value function and feedback control policy by resorting to the well-known critic-actor approximators. For instance, by using the certainty equivalence property, a linear system with random delays and packet losses has been transformed into a time-varying one, whose system and control matrices depend on a stochastic variable. Based on accessible data, these matrices have been estimated in [54] with the help of -learning and exploration noises (guaranteeing the PE condition). Then, a -learning algorithm combined with a dropout Smith predictor has been designed in [55] to solve the optimal control problems with network-induced dropouts. Very recently, a Bernoulli-driven HJB equation has been first developed in [53] to deal with optimal control problems without both a priori knowledge of system dynamics and the probability models of packet dropouts. These results promote future in-depth research and applications of ADP control in the presence of network-induced phenomena.

3.1.2. ADP Control Subject to Cyber Attacks

As we know, the open network may be subject to external malicious attacks. Generally speaking, cyber-attacks, according to the mathematical descriptions, are mainly divided into two categories: denial of service (DoS) attacks and deception attacks. Noting that the replay attacks are a special case of deception attacks. Specifically, DoS attacks refer to the communication transmission being blocked, that is because the communication channel is occupied or consumed by a large amount of useless data of the attacker, so the sampling data cannot be obtained at the moment of being attacked. Deception attacks can covertly manipulate data packets in the communication network, to achieve the purpose of falsifying or altering data, thereby compromising the integrity and credibility of the data.

It is worth mentioning that some preliminary efforts have been put forward to defend against the effects of cyber attacks in the ADP framework. When an attack occurs, system states (crucial for the analytic optimal controller) cannot be collected, and the iteration error of the cost function usually becomes bigger than that under attack-free cases. As such, this increment should need to be counteracted in the attack-free case. In light of this idea, a robust optimal output regulation problem has been handled in [56], in which the gap among RL, robust ADP, output regulation, and small-gain theories has been bridged. Furthermore, a lower bound has been found for the DoS attack duration. Besides, an observer with resilient requirements can be designed to break through this restriction. For instance, instead of using probabilities to describe DoS attacks, a sufficient condition has been received to design an NN-based observer via the input-to-state stability (ISS) property and average dwell time method of switched systems, and then the near-optimal controller has been obtained by means of the estimated state in [57].

When a deception attack is a concern, some compensations should be employed to reduce the impact of attack-induced errors. For instance, a robust and resilient controller has been construed that consists of two parts: an ideal optimal sub-controller for nominal systems and a compensation sub-controller related to the fictitious dynamical system in the cooperation interaction framework combined with ADP technique [58]. According to Lyapunov methods, the uniformly ultimate boundedness has been disclosed and the resilience has also been guaranteed in the presence of malicious attacks. Then, a model-free decentralized control scheme has been developed in [59], where the system dynamics, the probability of injection attack, and the boundary of interconnection are used as known information. Furthermore, the optimal control has been handled in [60] based on the two-player zero-sum game, where deception attacks have been approximated by a NN. Note that ADP-based control subject to cyber attacks still lies in the infant stage and deserves to be further investigated in a comprehensive and thorough manner.

3.2. ADP Control with Communication Protocols

3.2.1. ADP Control with Event-Triggering Protocols

As a special communication protocol, ETM has been widely applied in NCSs to efficiently relieve the limitation in computation and communication resources. Specifically, an ETM decides when or how often sampling control operations should be implemented based on some predefined events. Different from time-triggered ADP control, the nature of ETM-based ADP is to selectively collect or transmit information. In this way, the control performance may be sacrificed in a sense while the computation cost or burden will be reduced and control efficiency also is improved. Therefore, the key to the design of an ETM-based ADP controller is to balance the relationship between the control performance and computational burden. While reducing the computational cost, the necessary performance of the system, such as stability and convergence, must be maintained. The available ETM among the ADP control fields can be roughly divided into two types: the static ETMs [14, 61-63] and dynamic ETMs [57, 64-69]. Under static ETMs, the threshold or parameter in triggering conditions keeps fixed and does not change with the triggering interval. On the contrary, the threshold or parameter in dynamics ETMs can be adaptively adjusted according to the change of monitored data, such that the occupation rate of communication resources can be further reduced as well as ensure the expected system performance. Now, let us review the latest development of ADP control issues with static ETMs or dynamic ETMs.

Under a static ETM, the system states are transmitted only when the event-triggered condition is violated, and kept unchangeable by a zero-order holder in the adjacent triggering interval. For example, an event-triggering condition can be found in [14] with the form

with

where  stands for the optimal cost,  stands for the system state received by the controller,  means a predetermined constant. Furthermore, the next triggering instant is organized by the following rule:

where  denotes the -th triggering instant. It is not difficult to see that static ETMs have relatively simple structures and are easy to be designed. Therefore, such an event-triggering method has been widely used in many CT optimal control issues to improve the resource utilization efficiency of communication networks. In addition, the desired event condition for CT nonlinear systems can also be derived by substituting the ideal solution of the HJB equation into the Lyapunov function, where the utility function is selected as  and the controller is assumed to be Lipschitz continuous, see [70] for examples. Recently, for nonlinear CT systems with extra constraints, the ETM-based structure for optimal control has been designed in [61] and a decentralized scheme of event-driven control has been investigated for systems with both mismatched interconnections and asymmetric input constraints [71]. Furthermore, an ADP algorithm has been introduced into the ETM-based paradigm to address CT zero-sum games [62-63].

The dynamic ETMs, different from traditional static ones, have the capability of increasing the minimum triggered interval dynamically under the same initial conditions. In ADP fields, dynamic ETMs are divided into two categories according to their expressions. The first one is to achieve dynamic triggering by introducing a non-negative (or strictly positive) auxiliary dynamic variable into the constructed triggered condition such that more significant data has the opportunity to pass the dam built by the newly adjusted threshold. For instance, the dynamic ETM condition is designed in [66] with the structure

where  is the gap with the latest transmitted measurement , and  is a predefined positive threshold. The auxiliary dynamic variable  is given by

where  and  are adjustable parameters, and the initial value satisfy . Then, the next triggering instant is decided by

Following this auxiliary variable philosophy in dynamic ETMs, some profound results in optimal control fields have been achieved to further reduce resource and computational consumption. For instance, considering both saturated inputs and faulted actuators, a fault-tolerant optimal control strategy under dynamic ETM cases has been studied in [66] for nonlinear DT systems. Furthermore, convergent analysis of the ADP algorithm as well as the stability analysis of the closed-loop system has been performed by means of the Lyapunov theory. Very recently, an ADP-based controller with a dynamic ETM has been developed in [57] for unknown DT nonlinear systems under DoS attacks, where an effective time division has been applied to handle the challenges from the coupled attack and triggering sequence. Further, when a time-varying fault is a concern, a fault-tolerant optimal control scheme in a distributed way has been developed in [64] to realize a guaranteed cost.

Another type of dynamic ETM, also called adaptive ETMs, has been widely employed in DT nonlinear optimal control to improve computational efficiency. Following the definition of the ISS-Lyapunov function of DT nonlinear systems, the adaptive ETM condition proposed in [65] is given by

where the triggering error is  and  is a Lipschitz condition coefficient of nonlinear functions. Compared with the dynamic ETMs based on auxiliary variables, the threshold of such an ETM is not determined by the rate of change of the triggering error. Surely, the expression of the adaptive ETM is more concise and easy to implement compared with the above type of ETM. For instance, this ETM has been designed in [65] and the HDP technique has been employed to attain the control requirement. It should be pointed out that the triggering is state-dependent to cater to the ideal optimal control law. As such, when performing the developed approach, the states of studied systems must be fully observable. However, in practical systems, the full-state information could be either infeasible or very difficult to be sampled. To overcome this difficulty, an observer has been integrated into the ADP framework to recover the system states from the measurable feedback [70]. Recently, considering control constraints and system uncertainties, the adaptively near-optimal control problem has been solved for the nonlinear system with the ISS attribute under an ETM-based GrADP framework [68] and the self-learning optimal regulation has been investigated in [72] for DT nonlinear systems.

3.2.2. ADP Control with Stochastic Communication Protocols

In the multiple access case to a common communication channel, information transmission will inevitably suffer from data collisions. To prevent the occurrence of data conflicts, an effective method is to ensure that only one node owns a token to transmit its data through the shared channel at each transmission moment by communication protocols, thereby restricting network access to improve network efficiency. The communication protocol can coordinate the transmission order of all network users, thus resulting in some scheduling behaviors, which unavoidably complicates the performance analysis and gain design of networked systems. Besides the ETMs, there are also three widely studied communication protocols, that is, the TOD protocol [73], the RR protocol [74], and the SCP[75]. Specifically, in the field of ADP optimal control, the existing results that consider a communication protocol mainly focus on the RR protocol and SCP. In what follows, we will survey the recent progress of these two protocol mechanisms.

The RR protocol is a class of typical time-division multiple access protocols or token ring protocols [76-77]. To alleviate the network congestion caused by limited bandwidth among the ADP optimal control domain, an RR scheduling protocol has been employed in [76] to periodically transmit data. Let  be the measurements collected by the -th sensor, and the received data  with zero-order holders [76] under RR protocols is modelled by

where  stands for the number of nodes,  marks the -th sensor node endowed the chance utilizing transmission channels. More specifically, " " refers to the non-negative remainder on division of the integer  by the positive integer . By defining  and , the actual  can be further organized as follows

where  with  being binary function. In light of such a model, some profound results have been proposed to generate the optimal controller in the past years. For instance, an RR-based resilient consensus strategy has been proposed in [78] for time-varying state-saturated multi-agent systems, where the desired near-optimal scheme has been derived by minimizing the cost function over the finite horizon. Furthermore, an interesting scheme (i.e. a near-Nash equilibrium control strategy) has been developed in [79] to effectively carry out the non-cooperative optimal control problem for DT time-varying networked control systems under the RR protocol and the ETM, where the control strategies can be obtained by the pseudo inverse and completing-the-square technique.

Different from RR protocols, the SCP is a typical representative of carrier sense multiple access with collision avoidance (CSMA/CA) protocols, which have been widely adopted in various communication systems. Recently, the optimal control subject to SCPss has also received ever-increasing research attention, and the development of typical various control issues has been achieved, such as, resilient control [80], output-feedback control [81] and near-optimal regulation [82]. Furthermore, to profoundly disclose the impact, a reasonable mathematical model of SCPs should be constructed. The essence of the SCP is that each node gets access tokens randomly. Specifically,  sensors in a data collection system have been randomly scheduled to transmit their measurements to controllers or filters, and such "random switching" behavior of node schedule can usually be characterized by a know Markov chain with the following predetermined transition rule

where  for  and . Under SCP, the actual received data  held by the zero-order-holder is expressed by

Similar to RR protocols, the actual received  is simplified as

Driven by SCPs, the resilient ADP-based control has been investigated in [80] for DT time-varying systems. Very recently, a novel ADP near-optimal strategy has been professionally exploited in [82] for nonlinear systems subject to both unknown dynamics and input saturations. To be specific, the closed-loop system possesses the inherent feature of protocol-induced switches, and an interesting NN-based observer by introducing an auxiliary term has been exploited to approximate the unknown nonlinear dynamics, where a set of switchable weight updating rules has been designed by gradient descent laws, and an adjustable parameter has been added to enhance the robustness of the system. It should be pointed out that the effect of the statistical characteristic of SCPs has been disclosed by reconstructing the considered cost function combined with the transition probability matrix.

3.3. The Applications of ADP Methods in Practical Systems

The unique structure of ADP technology brings great potential and advantages in solving the optimal control problems of complex nonlinear systems. The application of optimal control based on the ADP method has expanded from the previous industrial control fields [83-87] (i.e. aluminum electrolysis production, and a boiler-turbine system in a wastewater treatment plant) to emerging high-tech fields [88-91] (i.e. aerospace, missile guidance, navigation systems, intelligent robots, smart grids, and intelligent transportation). However, the results of ADP optimal control application considering communication constraints are few, and the existing research results are briefly sorted out below.

In the fields of intelligent robots and intelligent transportation, an ETM-based predictive ADP algorithm has been proposed in [92] for path planning for autonomous driving of unmanned ground vehicles at intersections; and an ADP framework has been developed in [93] to achieve ideal control of smart vehicles where a source coding scheme has been applied to vehicle communication. When the aircraft application is a concern, an observer designed to [94] and [95] has been utilized to identify the accurate model of hypersonic vehicles in the re-entry stage, and then the optimal attitude tracking problem of the hypersonic vehicle has been solved under the framework of the ADP algorithm. In addition, a distributed optimal cooperative control strategy has been applied to the simultaneous collision guidance system of multiple missiles in [96], and it was verified that multiple missiles can hit the target simultaneously.

In the fields of power systems, a supplementary ADP idea has been utilized in [97] to compensate for the traditional controller to improve the system performance of a load frequency control problem in the existence of dynamic ETM and DoS attacks simultaneously. Furthermore, the same idea in the framework goal representation HDP has been utilized in [98] to discuss load frequency control with logarithmic quantization, where the conditions of learning parameters in weight update rules have been received.

4. Conclusions and the Future Works

This paper provided a comprehensive overview of ADP-based control of networked systems with unknown dynamics and communication constraints. First, some typical ADP structures and algorithms have been summarized and the related merits have been disclosed. In addition, the state-of-the-art results have been systematically investigated according to the constraint types (i.e. network-induced phenomena, cyber-attacks, ETMs as well as other communication protocols). Finally, applications of ADP-based control in various fields have been disclosed. In what follows, future topics on ADP-based control issues are lighted as follows.

● Innovate ADP algorithms and structures

With the continuous development and innovation of computer technology, it is very necessary to absorb effective learning algorithms in the field of machine learning to develop innovative ADP algorithms and structures that save computing resources and meet higher control performance requirements. This will be under the hot research direction of ADP control theory. Moreover, the use of communication protocols makes the system information incomplete, and hence the development of new ADP algorithms and structures is of great significance to deal with the incomplete information.

● Effects of approximation errors

The ADP-based algorithm is usually implemented via a set of neural networks, which is inevitably accompanied by approximation errors affecting the control performance of closed-loop systems. Furthermore, there are identified errors between the NN-based model and the actual project. However, in the current study, these errors have not been paid enough attention to. Therefore, developing a method to eliminate the error, or considering the controller design when the error exists, will be a direction for the future optimal control of networked systems.

● Data-driven ADP optimal control

Mechanistic modeling of practical systems becomes more difficult due to the widespread existence of nonlinearities, complex structures, and unknown parameters. Furthermore, NN modeling based on historical data could not be suitable for scenarios with changes in system information due to the weak generalization ability and local over-fitting. As such, data-driven adaptive optimization control under communication protocols will be one of the future hot research directions. For this topic, a critical challenge is how to disclose the impact of the adopted protocols whose physical model cannot be effectively reflected via data.

● Distributed ADP control with communication constraints

Benefiting from the utilization of communication networks, the deployment of modern industrial systems is moving from a centralized structure to a distributed one. Some interesting results have been developed and applied in smart grids, intelligent transportation, and so forth. The distributed deployment intensifies the complexity of network communications and promotes high control and design requirements, such as scalability and global/local optimality. There is no doubt that such a frontier research topic urgently needs to be put forward with great effort.

● ADP-based applications to more complex scenarios

With the rapid development of science and technology, many fields of technical applications have emerged, including intelligent industry, hybrid energy systems, autopilot driving, etc. This emerging area presents characteristics of high complexity, good intelligence, and high control performance requirements. The theory of ADP technology has evolved, and at the same time, its unique structure brings great potential in solving practical control problems. As a result, how to effectively and intelligently apply ADP to more complex scenarios to solve complex and practical control problems is the direction for more researchers going forward.

Author Contributions: Xueli Wang and Derui Ding: conceptualization; Ying Sun: investigation ; Xueli Wang: writing—original draft preparation; Xueli Wang and Ying Sun: writing—review and editing; Derui Ding: funding acquisition.

Funding: This work was supported in part by the Australian Research Council Discovery Early Career Researcher Award (DE200101128).

Conflicts of Interest: The authors declare no conflict of interest.